Usando um elemento cilíndrico, mostre que a relação de Stokes da viscosidade resulta nas seguintes componentes da tensão cisalhante:
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Determinando a taxa de tensão cisalhante no plano
Usando a seguinte expressão para determinar a taxa de tensão cisalhante nesse plano
Passo 2
O diagrama mostra a tensão cisalhante no plano
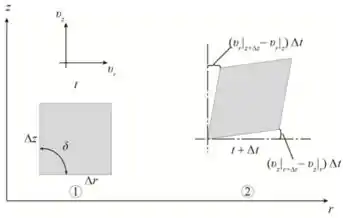
Passo 3
Determinando a tensão cisalhante no elemento
Usando a relação seguinte para determinar a tensão cisalhante no plano
Aqui, a viscosidade do fluido é e a taxa de mudança na tensão cisalhante é
Substituindo a expressão de obtida no final do Passo 1 na equação para
Passo 4
Determinando a taxa de tensão cisalhante no plano
Usando a seguinte expressão para determinar a taxa de tensão cisalhante nesse plano
Passo 5
O diagrama mostra a tensão cisalhante no plano
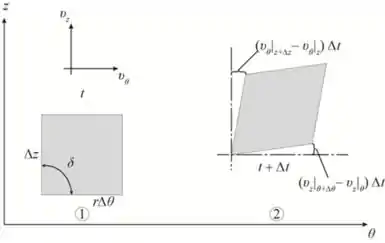
Passo 6
Determinando a tensão cisalhante no elemento
Usando a relação seguinte para determinar a tensão cisalhante no plano
Aqui, a viscosidade do fluido é e a taxa de mudança na tensão cisalhante é
Substituindo a expressão de obtida no final do Passo 4 na equação para
Passo 7
Determinando a taxa de tensão cisalhante no plano
Usando a seguinte expressão para determinar a taxa de tensão cisalhante nesse plano
Passo 8
O diagrama mostra a tensão cisalhante no plano
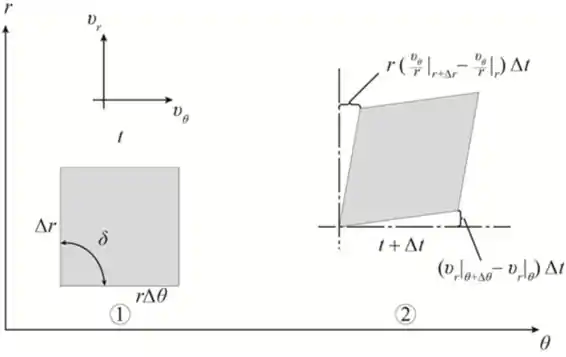
Passo 9
Determinando a tensão cisalhante no elemento
Usando a relação seguinte para determinar a tensão cisalhante no plano
Aqui, a viscosidade do fluido é e a taxa de mudança na tensão cisalhante é
Substituindo a expressão de obtida no final do Passo 7 na equação para