Usando o vetor velocidade do problema anterior, determine (a) a equação da linha de corrente passando pelo ponto (2, 1); (b) o volume de escoamento que cruza uma superfície plana conectando os pontos (1, 0) e (2, 2).
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
a) escrevendo a expressão para o vetor velocidade em um fluxo bidimensional
Aqui, os vetores unidade nas direções e são e , respectivamente
Derivando o eixo com respeito ao eixo na expressão do vetor velocidade
Aqui, os componentes de velocidade nas direções e são e , respectivamente
Passo 2
Integrando em ambos os lados da equação obtida no Passo 1
Aqui, a constante de integração é
Calculando o calor da constante no ponto da Equação obtida no começo desse passo
Substituindo para e para
Passo 3
Substituindo o valor encontrado para na equação para achar a equação da linha de corrente passando pelo ponto
Passo 4
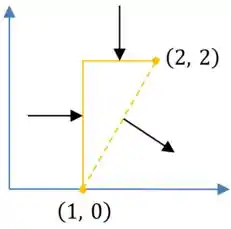
b) mostrando a superfície do plano conectando os pontos e
Passo 5
Calculando o volume do fluxo que atravessa uma superfície plana conectando os pontos e
Usando os pontos conectados e e integrando a equação acima