Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Munson, Mecânica dos Fluidos- Ed: 4º - Capítulo 5.Problemas - Ex. 12

A vazão de ar na seção de alimentação de um compressor é 30   m 3 / m i n (o ar está na condição padrão). A relação de compressão ( p s a í d a / p e n t r a d a ) , é 10 para 1 e nós sabemos que ρ / ρ n permanece constante durante o processo de compressão (com n = 1,4 ). Determine qual o diâmetro mínimo do tubo de descarga do compressor sabendo que a velocidade média na seção de descarga do compressor não deve exceder 30   m / s .

Passo 1

Bom! Mais uma aí, galera!

Pra começar vamo fazer um desenho bacana pra entender melhor o que tá acontecendo e onde os dados do enunciado tão inseridos...

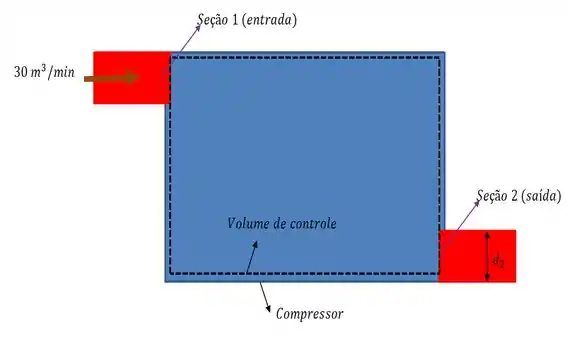
Vimos na teoria que para um fluido em fluxo constante e permanente o que entra tem que ser igual ao que sai.

Assim a massa que entra é igual a tudo que sai:

m ˙ e n t r a d a = m ˙ s a í d a

ρ e n t r a d a Q e n t r a d a = ρ s a í d a Q s a í d a

Onde...

Q e n t r a d a = > v a z ã o   n a   e n t r a d a

Q s a í d a = > v a z ã o   n a   s a í d a

Como...

p s a í d a p e n t r a d a = 10 1 = 10

E usando a relação abaixo...

ρ s a í d a ρ e n t r a d a = p s a í d a p e n t r a d a 1 n

ρ s a í d a ρ e n t r a d a = 10 1 1,4

ρ s a í d a ρ e n t r a d a = 5,1795

Então, temos que...

Q e n t r a d a = 5,1795 Q s a í d a

Passo 2

A gente sabe que a vazão de ar na seção de alimentação do compressor é 30   m 3 / m i n . Convertendo em m 3 / s :

Q e n t r a d a = 30   m 3 / m i n = 0,5   m 3 / s

Obtemos que...

Q s a í d a = Q e n t r a d a 5,1795

Q s a í d a = 0,5   m 3 / s 5,1795

Q s a í d a = 0,0965

Como a vazão é dada pelo produto da área pelo velocidade do fluido...

Q s a í d a = V s a í d a A s a í d a

E sabemos que a velocidade média ( V s a í d a ) na seção de descarga do compressor não deve exceder 30   m / s , então...

A s a í d a = Q s a í d a V s a í d a

π 4 d 2 = Q s a í d a V s a í d a

d = 4 Q s a í d a π V s a í d a

Substituindo os valores numéricos...

d = 4 Q s a í d a π V s a í d a

d = 4 ⋅ 0,0965 π ⋅ 30

d = 0,064   m

d = 64   m m

Obtemos nossa resposta!

Sucesso, rapaziada!

Resposta

d = 64   m m