5.30. Quando dois discos de hóquei idênticos, com ímãs repelentes, são mantidos juntos sobre uma mesa tipo “colchão de ar” e liberados, eles se afastam movendo-se em sentidos opostos com uma determinada velocidade, v. Considere agora que a massa de um dos discos seja dobrada, e o procedimento repetido.
a. A partir da terceira lei de Newton, derive uma equação que mostre como se compara a velocidade final do disco de massa dobrada com a velocidade do outro.
b. Calcule o valor da velocidade do disco de massa dobrada se o outro disco se move afastando-se a 0,4 m/s.
Passo 1
Beleza a situação é a seguinte:
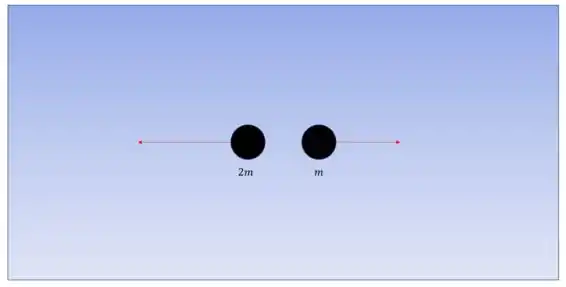
Segundo a terceira lei de Newton, os dois discos sofrem força de mesma intensidade. Bom, a partir daí podemos escrever uma equação para a aceleração dos discos, vamos chamar o disco de massa dobrada de disco 1:
E
Se a gente divide as duas equações temos:
Ou seja:
A aceleração do disco mais massivo é metade da aceleração do disco mais leve.
A gente pode usar isso agora para calcular a velocidade final, vamos supor que a velocidade inicial dos dois discos seja zero.
E
De novo temos:
Mas a gente sabe que
Então
A velocidade final do disco de massa dobrada é o dobro da velocidade final do outro.
Passo 2
Vamos calcular a velocidade , agora que é dado: