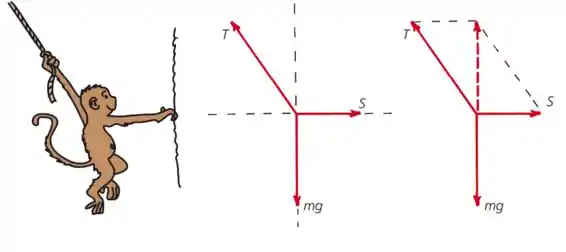
5.69. Com referência ao macaco Mo da Figura 5.26, qual será o módulo do vetor S se a corda que sustenta Mo for vertical? Se a corda fosse horizontal, de que maneira o vetor S seria diferente? Por que os dois vetores T e S não podem ser horizontais?
Passo 1
Vamos lá, dá uma olhadinha na figura 5.26 antes de continuar aqui.
Se a corda fosse vertical, os vetores ficariam assim:
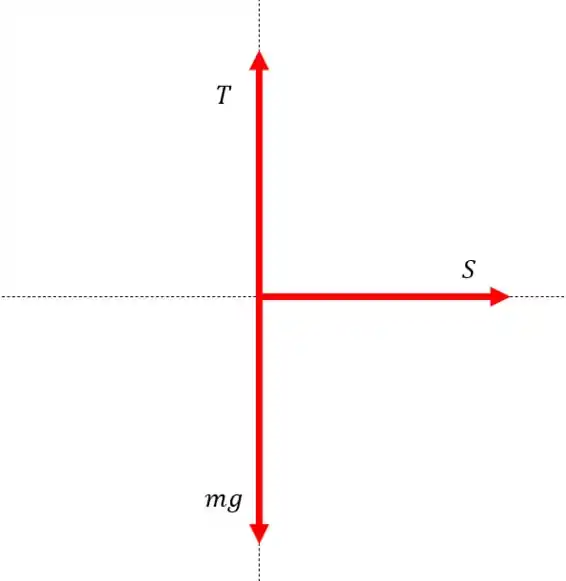
Olha só, o macaco está em repouso, isso está escrito no livro. Então a força resultante desses três vetores tem que ser zero.
Olha só, os vetores e estão na mesma direção, então eles podem se cancelar, mas o vetor e paralelo aos dois outros vetores, isso significa que nenhuma componente do vetor pode ser somada ou subtraída dos outros dois. Então o vetor tem que ser nulo. Olha só, e se cancelam, e o vetor não consegue se cancelar com ninguém, então, o único jeito do macaquinho continuar em repouso é se o vetor for nulo.
Passo 2
Agora, se a corda for horizontal, a gente teria isso:
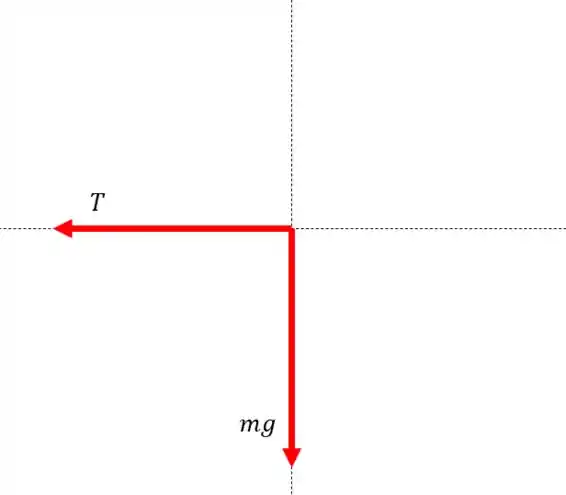
O vetor teria que entrar nessa configuração de forma que a resultante fosse zero. O que a gente pode fazer é somar e , e se esse vetor novo for igual e contrário ao vetor , garantimos que a força total é zero.
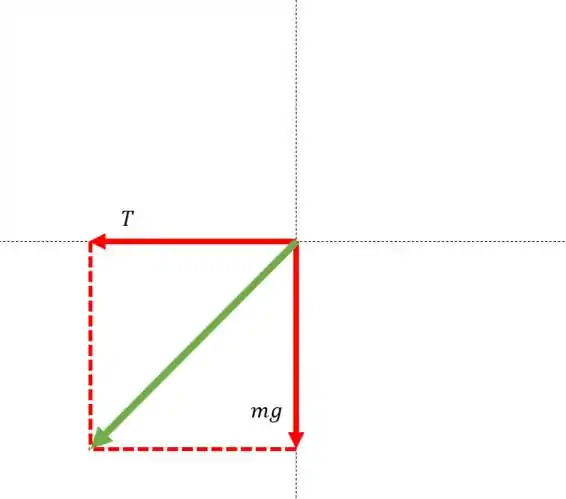
Então o vetor fica:
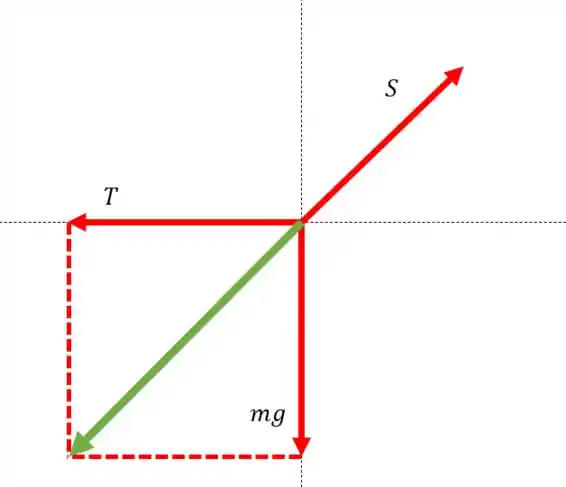
O vetor tem que se cancelar com o vetor resultante da soma entre e .
Passo 3
Agora vamos ver o que aconteceria se os vetores e fossem horizontais:
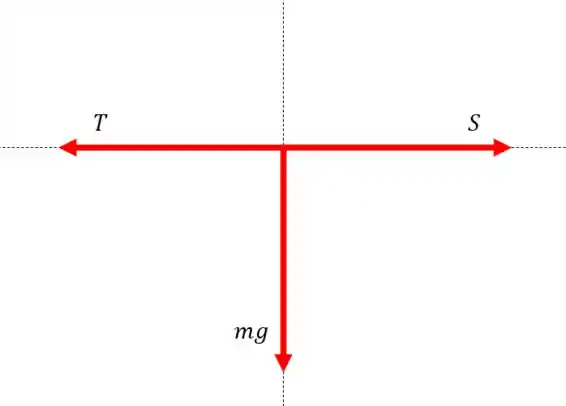
Agora e podem se cancelar, mas nenhuma componente do vetor pode ser cancelada, então se existir um vetor diferente de zero, vai existir uma resultante. No caso anterior, tem como não haver o vetor , mas não tem como não haver o vetor , a Terra sempre puxa o macaco, e por isso é impossível que a corda fique horizontal.
Resposta
Se a corda for vertical o módulo de é zero.
Se a corda for horizontal o vetor tem que se cancelar com o vetor resultante da soma entre e .
Se e forem horizontais, o vetor teria que ser zero, mas isso é impossível.