Um aluno deseja determinar os coeficientes de atrito estático e cinético entre uma caixa e uma prancha. Ele coloca a caixa sobre a prancha e lentamente vai levantando uma das extremidades. Quando o ângulo de inclinação faz 30° com a horizontal, ela começa a deslizar, descendo pela prancha cerca de 2,5 m em 4,0 s. Quais os coeficientes de atrito determinados?
Passo 1
Fala aí! A primeira coisa que vamos fazer para resolver esse tipo de questão é desenhar o que o enunciado nos descreve e anotarmos todas as forças que conseguirmos encontrar atuando nos corpos.
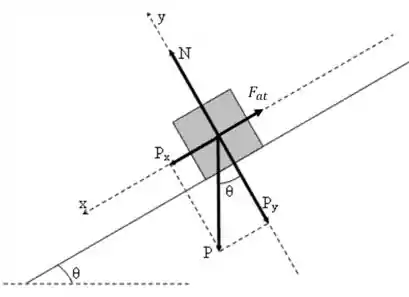
Beleza, depois disso, vamos relembrar como calculamos a força de atrito. Se você se lembrar, ela é expressa pelo produto entre o coeficiente de atrito e a força normal.
Mas por enquanto não conhecemos nenhum desses caras, então temos que procurar outro caminho.
Passo 2
Quem traz pra gente a solução é nosso grande amigo Newton, na forma da sua segunda lei. Lembra o que ela afirma? A força resultante que atua sobre um corpo é igual ao produto de sua massa pela aceleração:
E quem é essa tal força resultante? Ora, se olharmos para o eixo x desenhado ali na figura acima, veremos que as únicas forças atuantes são a força de atrito e a componente em x do peso. Portanto, podemos reescrever assim:
Vamos reescrever esse em termos do peso. Faremos isso por meio das relações trigonométricas do triângulo retângulo (é só olhar pra aquele ângulo ali na figura).
Agora podemos voltar na última equação e substituir e por suas respectivas expressões.
Passo 3
Para melhorarmos isso aí, vamos, agora, olhar para as forças atuantes no eixo y lá na figura. Consegue perceber que a força normal deve ser igual à componente ? Isso porque o corpo não se desloca nem pra lá nem pra cá no eixo y. Então:
A equação do passo anterior fica assim:
Vamos reorganizar isso aí para podermos isolar o coeficiente .
Como o peso corresponde ao produto da massa pela gravidade, podemos substituir e cancelar a massa em todos os termos:
Passo 4
Agora só precisamos encontrar essa aceleração, já que todos os outros valores são conhecidos. Um meio de encontrá-la se dá pela função horária do espaço, a qual é expressa da seguinte forma:
Como a velocidade inicial é zero, ficamos com a distância percorrida é igual à aceleração vezes o tempo ao quadrado dividido por dois. Bora substituir esses valores e ver no que dá
Agora podemos voltar na equação do passo anterior.
Afinal, esse é o coeficiente de atrito cinético ou estático? Ora, se utilizamos uma aceleração diferente de zero nos nossos cálculos, só pode ser o cinético, pois isso indica que o corpo está em movimento.
Passo 5
Para finalizar, bora encontrar o bendito do coeficiente de atrito estático, então. Mas relaxa que 99% do nosso trabalho já está pronto.
Olha só, nos passos anteriores, encontramos uma equação que descreve os coeficientes de atrito deste caso e, como sugeri no último passo, o coeficiente de atrito estático deve ser calculado com uma aceleração igual a zero. Portanto, tudo o que precisamos fazer aqui é o seguinte:
Com :
Resposta
O coeficiente de atrito estático vale 0,58 e o cinético vale .