Um avião voa 480 km da cidade A para a cidade B na direção leste em 45,0 min e, depois, voa 960 km da B para a C na direção sul em 1,50 h. (a) Qual o vetor deslocamento que representa a viagem total? Quais são o vetor velocidade média e (c) a velocidade escalar média nesta viagem?
Passo 1
Fala aí! Bora começar desenhando a trajetória deste avião de acordo com os passos fornecidos pelo enunciado.
Para começar, ele se deslocar 480 km na direção leste.

Depois disso, 960 km para o sul.
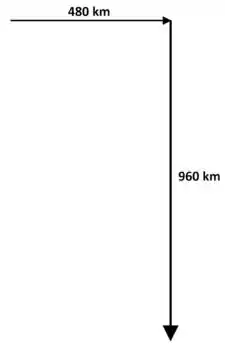
E o vetor deslocamento é aquele que parte em linha reta do ponto de origem até o final:
![]()
Para encontrarmos seu módulo, vamos reparar que ele herda a componente em x do primeiro movimento e a em y do segundo. Assim, as componentes do vetor deslocamento são:
E, pela definição do módulo de vetor, basta fazermos o seguinte:
Falta informarmos a direção deste vetor. Faremos isso por meio daquele ângulo ali em cima, se liga:
Se olharmos a cotangente de 2, acharemos o ângulo . Isso significa que o vetor deslocamento está em uma direção a ao sul do leste.
Passo 2
Beleza, agora vamos encontrar a velocidade vetorial média. Para isso, basta dividirmos o módulo do deslocamento pelo tempo total gasto durante o percurso, tomando cuidado para usarmos sempre as mesmas unidades.
A direção desse cara é sempre a mesma do deslocamento.
Passo 3
Para finalizar, vamos encontrar a velocidade escalar média. Esse cara é bem parecido com o anterior, a diferença é que aqui utilizamos a distância total percorrida.
Como aqui dividimos um escalar por outro, não faz sentido falarmos em direção.
Resposta
(a) na direção 63,44º ao sul do leste.
na mesma direção do vetor deslocamento.
(b)