Um balão, em 3,50 h, se desvia 21,5 km ao norte, 9,70 km a leste e 2,88 km acima do seu ponto de decolagem no solo. Determine (a) o módulo da sua velocidade média e (b) o ângulo que a sua velocidade média faz com a horizontal.
Passo 1
Fala aí! O primeiro passo pra resolver essa aqui é ficar esperto pra não dar bobeira e errar logo no começo. Se liga, pra calcular a velocidade média, precisamos de um valor de distância e um de tempo, concorda? O tempo foi dado pelo enunciado, são 3,50 horas. Quanto a distância, será que basta somar cada um dos desvios feitos pelo balão? Não!
Cara, se usarmos a distância total percorrida, que é uma grandeza escalar, vamos obter a velocidade escalar média. O que queremos é o vetor velocidade média, por isso devemos utilizar o vetor deslocamento nos nossos cálculos.
Para ilustrar melhor, dá só uma olhada no gráfico a seguir:
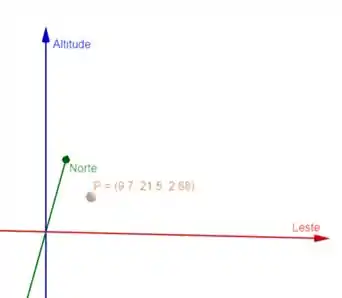
Consegue perceber que não é como se o balão se deslocasse 21,5 km ao norte, 9,70 km a leste e depois 2,88 km para cima, mas na verdade ele se desloca em todas essas direções ao mesmo tempo? Então, na verdade, o que precisamos encontrar é aquele vetorzinho em preto ali:
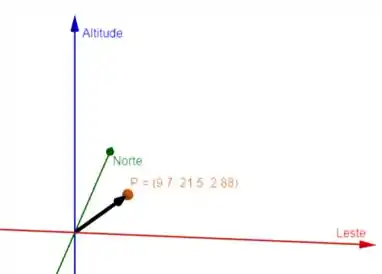
Beleza, e como fazemos isso, afinal? Muito simples, se lembrarmos que o módulo de um vetor é a raiz quadrada da soma de cada uma de suas componentes ao quadrado, e que as componentes desse tal vetor deslocamento são os próprios valores fornecidos pelo enunciado, podemos fazer o seguinte:
Finalmente, podemos calcular a bendita velocidade média, da seguinte forma:
Passo 2
Agora, nos falta encontrar o ângulo desse cara em relação à horizontal. Se liga:
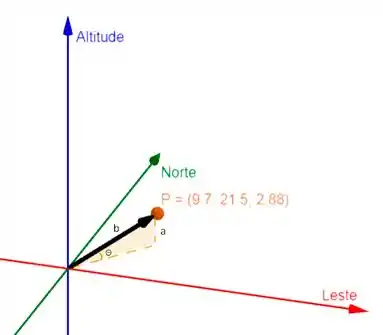
Reparou no triângulo retângulo formado ali? Aquele cateto menor, marcado como a, é o deslocamento para cima e mede 2,88 km. A hipotenusa, marcada com um b, é o vetor deslocamento que acabamos de calcular. Podemos relacionar esses dois caras por meio do seno do ângulo , que é o que queremos encontrar.
Agora, basta acharmos o arco cujo seno vale 0,121, aí teremos nossa resposta.
Resposta
(a) 6,79 km/h.
(b) 6,96º.