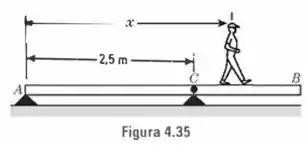
A barra uniforme da Fig. 4.35 é de de comprimento e pesa . Há um ponto fixo em torno do qual a haste pode girar. A haste está repousando sobre o ponto . Um homem pesando está andando sobre a barra, partindo de . Calcule a distância máxima que o homem poderá afastar-se de e ainda manter o equilíbrio. Represente num gráfico a reação no ponto em função da distância .
Passo 1
E aí, beleza?? Vamos calcular a reação normal em função da posição para, então, encontrar a distância máxima que o homem pode estar do ponto . Tomando o torque resultante em torno do ponto , sabendo que o peso dista de desse ponto, temos:
Portanto, a função se anula em , sendo essa a maior distância que o homem pode estar antes que a barra tombe.
Passo 2
O gráfico da força em função de é:
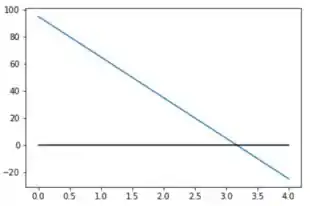
Em que a força é a reta azul, enquanto a preta corresponde à reta .