Um bloco de 3,57 kg é puxado com velocidade constante por uma distância de 4,06 m em um piso horizontal por uma corda que exerce uma força de 7,68 N fazendo um ângulo de 15,0° acima da horizontal. Calcule (a) o trabalho executado pela corda sobre o bloco e (b) o coeficiente de atrito dinâmico entre o bloco e o piso.
Passo 1
Fala aí! Antes de começar a resolver questões desse tipo, é sempre bom tentar desenhar o que o enunciado descreve e anotar todas as forças atuantes sobre os corpos, isso vai ajudar bastante na visualização do problema.
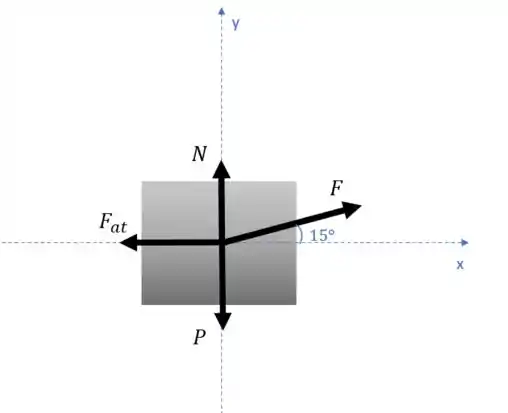
Beleza, anotei ali: a força de atrito , o peso (P), a normal (N) e a força com que o bloco é puxado . Já aproveitei para decompor essa força em suas componentes em x e y também.
Para encontrarmos o trabalho realizado pela corda, vamos usar a seguinte expressão:
Essa expressão diz que o trabalho é igual ao produto entre a força, o deslocamento e o cosseno do ângulo entre essas duas variáveis anteriores. Bora aplicar os valores e ver no que dá.
Passo 2
Para encontrar o coeficiente de atrito, vamos ter que olhar pra essa expressão aqui:
Ela afirma que a força de atrito é igual ao produto entre o coeficiente de atrito e a normal. O problema é que ainda não conhecemos o valor da força de atrito, então temos que encontrar um jeito de achá-la.
Nossa saída vem por meio da segunda lei de Newton, aquela que diz que a força resultante é igual ao produto da massa e da aceleração. Se liga:
Se olharmos lá para o eixo x na figura acima, veremos que temos a força de atrito de um lado e do outro conseguimos decompor aquela força F ali. Olha só, se usarmos as relações trigonométricas do triângulo retângulo, vamos encontrar o seguinte:
Agora, voltando na lei de Newton, vamos dizer que a força resultante é a soma desse cara aí e da força de atrito, que aponta no sentido oposto (por isso fica negativo).
Como a velocidade do bloco é constante, a aceleração vale zero. Logo:
Passo 3
Se repetirmos o processo do passo anterior, vamos encontrar que a força resultante no eixo y é a soma entre a normal, o peso e a componente em y de F.
Vamos substituir os valores para encontrar N.
Agora sim, podemos voltar lá naquela expressão da força de atrito e substituir os valore que encontramos.
Resposta
(a) 30,1 J.
(b) 0,23.