Um bloco de gelo de 45 kg escorrega por uma rampa sem atrito de 1,5 m de comprimento e 0,91 m de altura. Um operário aplica uma força no bloco, para cima, paralelamente à rampa, com uma intensidade suficiente para que ele desça com velocidade constante. Determine (a) a força exercida pelo operário, (b) o trabalho executado sobre o bloco pelo operário, (c) o trabalho executado sobre o bloco pelo seu peso, (d) o trabalho executado sobre o bloco pela força normal exercida pela rampa e (e) o trabalho total executado sobre o bloco.
Passo 1
Fala aí! Antes de começar a resolver questões desse tipo, é sempre bom tentar desenhar o que o enunciado descreve e anotar todas as forças atuantes sobre os corpos, isso vai ajudar bastante na visualização do problema.
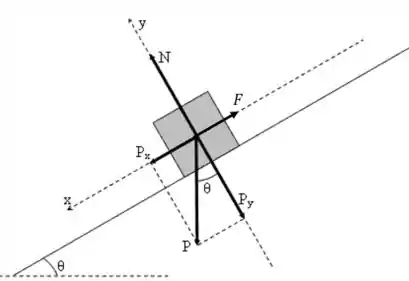
Beleza, agora vamos seguir o passo a passo pra não nos perdermos.
Aquela força ali no desenho, apontando no sentido de subida na rampa, é exercida pelo operário. Repare, também, naquele vetorzinho oposto a ela; ele é a componente do peso paralela ao eixo da rampa.
Vamos relembrar do que dizia a segunda lei de Newton:
Essa expressão afirma que a força resultante sobre um corpo é igual ao produto de sua massa e da aceleração. Pois bem, o enunciado nos informou que o bloco desce a rampa com uma velocidade constante, isso quer dizer que sua aceleração é zero.
Mas quem é essa tal força resultante? Ora, é a soma de todas as forças que atuam no eixo x, neste caso, temos somente a força F e a componente .
Como escolhemos o sentido de descida da rampa como o semieixo x positivo, fica positivo e fica negativa, tranquilo?
Perfeito! Mas ainda precisamos melhorar isso aí para encontrar um valor para a força F. Nossa saída vai ser utilizar as relações trigonométricas do triângulo retângulo; é só olhar para a figura ali em cima e reparar no triângulo pequeno formado nas forças lá no bloco. Isso vai nos permitir decompor o peso da seguinte forma:
Passo 2
Chegamos em mais um impasse, pois também não conhecemos o valor de . Mas não se preocupe, vamos descobrir quem é esse cara bem facilmente.
Novamente, olha na figura anterior, dessa vez, foca no triângulo maior formado pela rampa. Reparou que o mesmo ângulo tá presente ali? Então, acontece que o enunciado nos informou o valor do comprimento e da altura da rampa, que correspondem ao cateto adjacente e ao cateto oposto, respectivamente. Portanto, podemos usar uma outra relação trigonométrica:
E para encontrarmos o valor de , basta acharmos o arco cuja tangente vale 0,606.
Passo 3
Agora sim, podemos voltar na expressão lá do passo um e substituir o valor que encontramos:
E, voltando na segunda lei de Newton:
Passo 4
Seguindo em frente, vamos tentar encontrar o trabalho realizado pelo operário sobre o bloco. Para isso, vamos antes relembrar como se calcula o trabalho de uma força:
Essa expressão diz que o trabalho é igual ao produto da força, do deslocamento e do cosseno do ângulo formado entre essas duas variáveis anteriores. Repare que, como o operário fornece uma força contrária ao sentido de deslocamento do bloco, o ângulo vai ser de 180°.
Beleza, mas ainda não conhecemos o valor do deslocamento, né? Para descobrirmos esse cara, vamos olhar novamente para o triângulo retângulo formado pela rampa. Dessa vez, vamos usar o teorema de Pitágoras para descobrir o valor da hipotenusa, que corresponde à distância percorrida pelo bloco.
Agora sim, vamos voltar na equação do trabalho.
Passo 5
Para encontrar o trabalho realizado pelo peso do bloco, o processo é muito parecido com o do passo anterior. Olha só, vamos olhar para a componente e substituir os valores na equação do trabalho.
Repare que, como a componente aponta no mesmo sentido do deslocamento, o ângulo formado dessa vez vale 0°.
Passo 6
Tá, esse foi o trabalho da componente x do peso, mas ainda falta a componente y, né? Cara, dá só mais uma olhada naquele desenho lá e tenta reparar no ângulo que forma com o deslocamento. Reparou? Dá só uma olhada em como fica a expressão do trabalho se formos jogar os valores:
![]()
Qual é o cosseno de 90°? Muito bem, é zero! Isso quer dizer que as forças perpendiculares ao movimento do corpo não exercem trabalho. Neste caso, isso vai se aplicar tanto para a componente em y do peso quanto para a força normal!
Resposta
(a) 228,58 N.
(b) -400,02 J.
(c) 400,02 J.
(d) 0 J.
(e) .