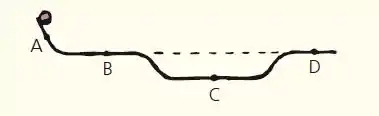
Uma bola é liberada a partir do repouso da extremidade esquerda do trilho metálico como mostrado abaixo. Considere que exista atrito apenas suficiente para o rolamento, mas que ele não diminua a velocidade. Ordene as grandezas abaixo, em cada ponto assinalado, em sequência decrescente quanto
- ao momentum.
- à EC.
- à EP.
Passo 1
Simbora!
Antes de ordenar, vamos ver como calcula essas alternativas.
Temos para o momento,
Para a energia cinética
E para a energia potencial
Show?! Vamos para as análises!
Passo 2
Para o momento, consideremos que como a bolinha desceu a rampa, ela ganhou velocidade, logo, em C teremos a maior velocidade, seguido por B e D com momentos iguais e A por fim, assim:
Se analisarmos quanto a energia cinética, no ponto C é onde a energia potencial foi toda convertida em cinética, seguido por B e D igualmente e por fim, A, assim:
Agora, por fim, quanto a energia potencial, A é o ponto mais alto, seguido por B e D e por fim, C, assim:
Resposta
Ei, a resposta está no passo a passo :)