Cargas q, 2q e 3q são colocadas nos vértices de um triângulo equilátero de lado “a” (fig). Uma carga Q de mesmo sinal que as outras três é colocada no centro do triângulo. Obtenha a força resultante sobre Q (em módulo direção e sentido).
Passo 1
Fala galera, tudo tranquilo? Esse problema requer um pouco de geometria entre outros conceitos. Iremos analisar cuidadosamente o triângulo dado no problema e com isso podermos chegar em nosso resultado.
Para começar, vamos tratar 3 retas em nosso triângulo onde passam pelo ponto centrado o qual se encontra a carga, A altura h do triângulo é dada por , caso você não consiga perceber isso, mostrarei de um jeito bem fácil. Outro ponto que devemos descobrir é o valor da reta “d” que é um valor arbitrário que depende de “a”. Após isso nós devemos apenas decompor os vetores e escrever as forças eletrostáticas em cada sentido dos versores î e ĵ.
Observe a figura abaixo para entender melhor o que irei falar.
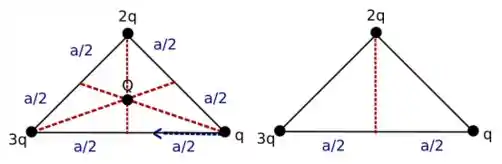
Vamos encontrar a altura “h”:
vamos olhar para o triângulo do lado direito e a reta vermelha na vertical. Ela é nossa altura “h”. Então, vamos por um ângulo teta no vértice onde a carga “q” se encontra. Sabemos que como dividimos nosso triângulo ao meio, e a soma dos ângulos internos de um triângulo são 180 graus, então como portanto.
. Agora precisamos encontrar o termo “d”. Esse “d” é a reta que cruza da direita para a esquerda passando pelo ponto central do triângulo. Dessa forma temos
podemos simplificar os elementos dividindo tudo por 4
.
Passo 2
Agora que encontramos as partes mais chatinhas de encontrar, iremos trabalhar com as forças eletrostáticas atuando na carga Q. Seguindo a imagem do lado esquerdo, vamos aplicar a força da carga q em Q chamaremos ela de força aqui o cosseno é negativo devido o sentido contrário ao eixo x (adotando o sentido positivo de x da esquerda para direita).
A força que a carga 3q exerce na carga Q é:
A força exercida pela carga 2q na carga Q é da forma:
. A força eletrostática em x é zero, pois não existe componente em x para a carga 2q. A componente Y é negativa devido ao sentido que a força está exercendo sobre a carga Q. Agora pegamos a resultante dessas forças e chegaremos em nossa resposta. Lembrando que:
Resposta
Pegamos as forças das componentes x referente ao versos î. Sendo este o vetor que nos interessa
A resposta no livro contém um 16 onde encontrei 12. Mas, refiz esse problema várias vezes, entretanto o valor não corresponde. Provavelmente há algum erro na resposta do livro. Você pode decompor os vetores de outras maneiras, mas o resultado ainda será diferente do livro.