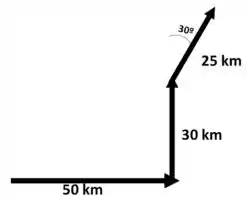
Um carro viaja 50 km para leste, 30 km para o norte e 25 km em uma direção 30º a leste do norte. Represente os movimentos do carro em um diagrama vetorial e determine o deslocamento total do veículo em relação ao ponto de partida.
Passo 1
Fala aí! Essa aqui é bem direta, né? Vamos desenhar seguindo as instruções do enunciado.
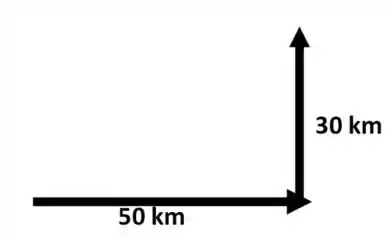
O primeiro movimento é de 50 km para o leste:
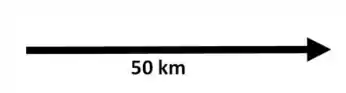
Em seguida, vamos 30 km para o norte.
O próximo movimento é 25 km a 30º a leste do Norte.
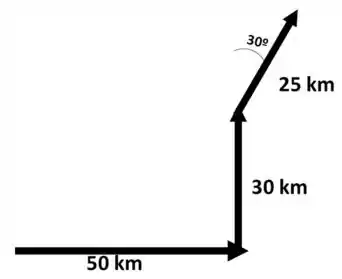
Tudo tranquilo, né? E o que queremos encontrar é o valor do deslocamento, que parte lá do ponto de origem até o final.
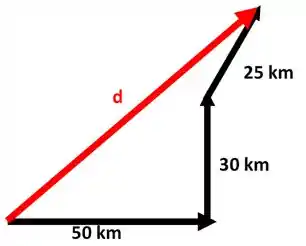
Passo 2
Beleza, agora precisamos pensar em como encontrar o módulo desse cara. Vamos fazer o seguinte, imagine se jogarmos esse desenho em um eixo cartesiano, a direção leste-oeste fica como o eixo x e norte-sul vira y, concorda?
Pois bem, consegue perceber que aquele vetor voltado meio que a nordeste tem uma partezinha no eixo x e outra em y? O que temos que fazer é encontrar exatamente o valor de cada uma dessas partes, é isso que se chama decomposição de vetores!
Olha só, vou chamar o vetor do primeiro movimento de A, o segundo de B e o terceiro de C, vamos olhar para cada um deles e identificar suas componentes em x e y. A e B são bem fáceis, pois só têm componentes e , respectivamente.
Agora, para C, vamos prosseguir da seguinte forma:
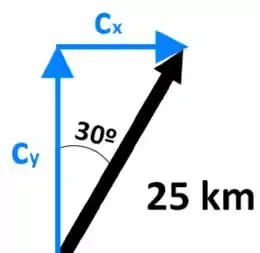
e são as componentes em y e x que queremos encontrar do vetor C. Como conhecemos aquele ângulo de , podemos utilizá-lo ao nosso favor, olha só:
Passo 3
Agora que encontramos as componentes do vetor que faltava, podemos encontrar o valor do deslocamento total. Temos dois caminhos: um geométrico – redesenhando o vetor deslocamento do passo 1, agora com as componentes e – ou por meio da definição do módulo de vetor, que é o que faremos aqui.
Se liga, nosso vetor deslocamento tem as seguintes componentes:
O módulo de um vetor é encontrado por meio da raiz da soma do quadrado de suas componentes.
Resposta