Certa melancia tem as seguintes coordenadas: x = -5,0 m, y = 8,0 m e z = 0 m. ache seu vetor posição (a) em notação de vetores unitários e (b) em função do seu módulo e da sua direção. (c) Represente o vetor num sistema de coordenadas dextrogiro.
Passo 1
Fala aí! Tá lembrado do que é essa notação de vetores unitários? É aquele sistema que utiliza as componentes vetoriais , o qual tem os coeficientes x, y e z como suas componentes escalares.
Então, para representarmos o vetor posição da melancia nesse sistema, basta escrevermos:
Passo 2
E como calculamos o módulo de um vetor tridimensional? Ora, se no plano fazíamos a raiz da soma de cada uma das componentes ao quadrado, aqui se mantém a mesma ideia, porém agora temos uma componente adicional.
Esse é o módulo do vetor posição, agora, vamos descobrir um jeito de informar sua direção. Dá só uma olhada no desenho seguinte:
![]()
Em vermelho, temos o vetor posição com seu módulo ao lado. Podemos encontrar aquele ângulo ali da seguinte forma:
Se olharmos qual a cotangente de 1,6, encontraremos um ângulo bem próximo de . Assim, podemos dizer que a direção do vetor posição é a aproximadamente do semieixo negativo.
Passo 3
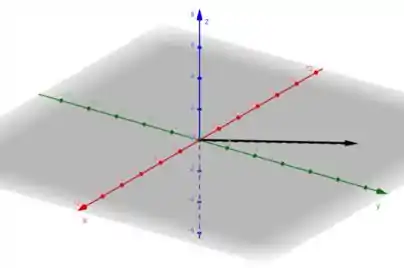
Para finalizar, vamos representar esse cara em um sistema de coordenadas dextrogiro. Como a componente z é nula, deve ser bem fácil fazer esse desenho:
Resposta
(a)
(b)
na direção a do semieixo x negativo.
(c)