O coeficiente de atrito cinético na Fig. 6-21 é 0,20. Qual a aceleração do bloco se (a) deslizar para baixo no plano inclinado e (b) se for dado um empurrão para cima, fazendo-o deslizar sobre o plano inclinado?
Passo 1
Fala aí! Essa questão parece meio vaga, né? Não nos foram fornecidas muitas informações, então teremos que dar a resposta em função das variáveis desconhecidas. Para começar, vamos escrever a força de atrito, que é expressa pelo produto entre o coeficiente de atrito e a força normal:
Feito isso, vamos olhar para a segunda lei de Newton, a qual afirma que a força resultante que atua sobre um corpo é igual ao produto de sua massa pela aceleração:
Agora, pensa aqui comigo: qual é a força resultante quando o bloco desliza para baixo? Vamos olhar pra imagem a seguir pra responder isso aí.
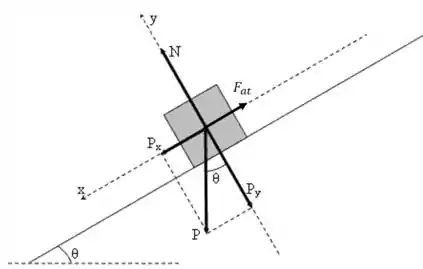
Fica mais fácil de visualizar assim, né? É a componente da força peso que aponta no sentido de descida da rampa menos a força de atrito. Para encontrar essa componente, é só usarmos as relações trigonométricas.
Então, ficamos com:
Passo 2
Para melhorarmos um pouquinho essa expressão, vamos voltar lá na força de atrito. Já conseguimos expressá-la em função da força normal, certo? Pois bem, repare no desenho como a normal e a componente em y do peso são as únicas forças atuantes no eixo Y, isso quer dizer que ambas têm exatamente o mesmo módulo.
E, como já vimos, podemos encontrar quem é por meio de relações trigonométricas.
Agora, vamos voltar naquela última expressão do passo anterior e melhorá-la.
O produto é igual ao peso , portanto, podemos colocá-lo em evidência.
Se cancelarmos as massas dos dois lados da equação, o que sobra é o seguinte:
Passo 3
Para finalizar, vamos ver o que aconteceria caso o bloco fosse empurrado plano acima. Antes de mais nada, vamos atualizar nosso desenho:
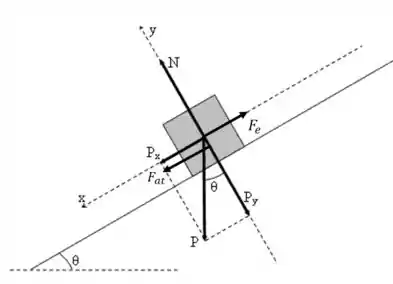
A grande diferença aqui é que surge uma força , a qual empurra o bloco para cima e, como consequência, a força de atrito agora aponta no sentido contrário. Então, nossa expressão da força resultante agora fica assim:
Aí basta substituirmos as expressões novamente.
Antes de encerrar, deixa eu fazer uma ressalva: como o enunciado não deixou muito claro, a expressão acima vale somente caso o bloco continue sendo empurrado para cima com a força constante . Agora, caso essa força forneça só o impulso inicial, e não continue agindo sobre o corpo, podemos tirá-la da equação. Aí ficaríamos com:
Resposta
(a)
(b) ou , dependendo da sua interpretação 😉.