Quando um cometa se aproxima do Sol, o gelo da superfície do cometa sublima, liberando íons e partículas de poeira. Como possuem carga elétrica, os íons são empurrados pelas partículas carregadas do vento solar e formam uma cauda de íons, retilínea, que aponta radialmente para longe do Sol (Fig. 33- 39). As partículas de poeira (eletricamente neutras) são empurradas para longe do Sol pela força da luz solar. Suponha que as partículas de poeira são esféricas, têm uma massa específica de 3,5 × 103 kg/m3 e são totalmente absorventes. (a) Que raio deve ter uma partícula para descrever uma trajetória retilínea, como a trajetória 2 da figura? (b) Se o raio da partícula é maior que o valor calculado no item (a), a trajetória se encurva para longe do Sol, como a trajetória 1, ou para perto do Sol, como a trajetória 3?
Passo 1
a) Para termos uma trajetória retilínea, as forças devem ser equilibradas. Então a força radiação deve equilibrar a força gravitacional:
Agora a massa da esfera pode ser reescrita como o produto da massa especifica pelo volume, enquanto que a área é de .
Simplificando e isolando o raio da esfera, temos:
Passo 2
Os dados que o problema nos traz e os tabelados necessários são:
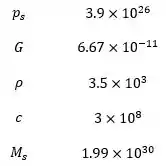
Substituindo os valores, temos:
Passo 3
b) A força de radiação varia com , por causa da área , enquanto que a força gravitacional com , por conta da massa, então quando o raio fica maior, a força gravitacional é maior e puxa a partícula para perto do sol, conforme a trajetória 3.
Resposta
Letra a)
Letra b)
Perto do sol, conforme trajetória 3.