Considere um paciente submetido a um tratamento de tração como indica a figura G.1.6.
Qual a máxima massa a ser utilizada para produzir a forca tênsil sem que o paciente se desloque ao longo da cama? Sabe-se que a massa desse paciente e 60kg, o coeficiente de atrito entre o mesmo e a cama e ,e o angulo que a forca tênsil forma com a horizontal e .
Passo 1
Primeiramente vamos fazer o diagrama de corpo livre, para esquematizar todas as forças que atuam no corpo:
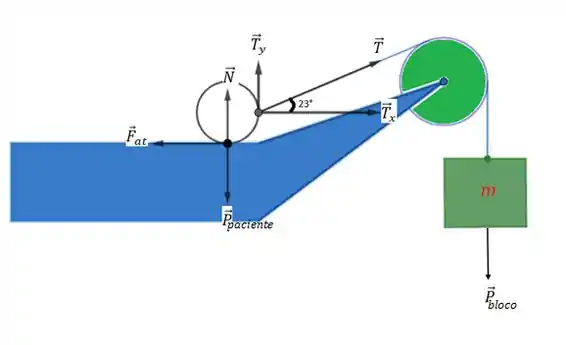
Com o DCL todo esquematizado, fica fácil ver todas as forças atuantes no sistema.
Considere a circunferência menor como a cabeça do paciente.
Passo 2
Para o corpo permanecer em repouso, analisando o DCL, temos que:
:
Passo 3
Agora vamos analisar as forças, em cada referencial:
Na horizontal:
Vamos analisar em particular, cada uma dessas duas forças:
Passo 4
A força de atrito é calculada em função da força normal :
é a componente horizontal da força tênsil :
Subst. , ficamos com nossa nova equação na horizontal:
Passo 5
Vamos calcular as forças na vertical:
Vamos analisar cada força da equação em particular:
Passo 6
é a componente vertical da força tênsil :
Subst. em temos então nossa relação na vertical:
Subst. :
Passo 7
Vamos analisar o bloco de massa :
O fio que sai da cabeça do paciente, é o mesmo que prende o bloco, a tensão no fio é igual nos dois pontos:
Podemos determinar a tensão no fio como:
é a força peso do bloco:
Então nossa tensão no fio é dada por:
Subst. :
Agora vamos isolar :
Passo 8
Simplificando dos dois lados, temos:
Tirando em evidência temos:
Subst. os valores numéricos chegamos que é:
Resposta