Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Griffiths - Mecânica Quântica- Ed: 2º - Capítulo 2.Problemas - Ex. 51

Considere o potencial

v x =   - h 2 a 2 m   s e c h 2   a x .

em que a é uma constante positiva e 'sech' indica secante hiperbólica.

a) Faça uma representação gráfica desse potencial.

(b) Verifique se esse potencial tem como estado fundamental

¥ 0 x = A sech ⁡ ( a x )

e calcule a sua energia. Normalize ¥ 0 e esboce um gráfico.

(c) Demonstre que a função

¥ k x = A i k - a t g h a x i k + a   e ∝ ,

(em que k √ 2mE / h, como sempre) resolve a equa- ção de Schrödinger para qualquer energia (positiva) E. Sendo que a tgh z -1 quando z → - ∞ ,

Isso representa, então, uma onda vinda da esquerda sem onda de acompanhamento refletida (isto é, sem termo exp(-ikr). Qual é a forma assintótica de ( ¥ k ( x ) em x grande positivo? Quais são R e T para esse potencial? Comentário esse é um exemplo famoso do potencial sem reflexão: toda particula incidente, independentemente de sua energia, passa diretamente.

Passo 1

a) Sabemos que teremos uma secante hiperbólica, Além disso, temos que o coeficiente angular, a, tem valor negativo, o que nos indica que x passa por uma queda de valor quando v(x) atinge seu valor mínimo. Assim, conseguimos concluir que o gráfico solicitado ficaria com o seguinte semblante:

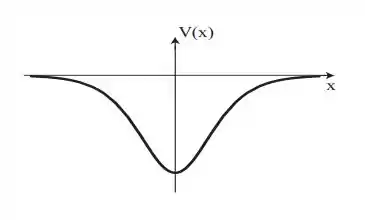
Passo 2

Agora, vamos resolver os cálculos solicitados. Antes de começar, é importante lembrarmos que a secante e a tangente hiperbólica estarão sendo representadas aqui, respectivamente, como sech e tgh. Logo, temos:

d ψ 0 d x = - A a sech ⁡ a x tgh ⁡ a x ;

E:

d 2 ψ 0 d x 2 = - A a ² - s e c h ( a x )   t g h ² ( a x ) + s e c h ( a x )   s e c h ² ( a x )  

H ψ 0 = - ħ 2 2 m d 2 ψ 0 d x 2   - ħ 2 a 2 m s e c h ² ( a x ) ψ 0

H ψ 0 = ħ 2 2 m   A a ² - s e c h ( a x )   t g h ² ( a x ) + s e c h ³ ( a x ) - ħ 2 a 2 m   A   s e c h ² ( a x )

H ψ 0 = ħ 2 a 2 A 2 m - s e c h ( a x ) t g h ² ( a x ) + s e c h ³ ( a x ) - 2 s e c h ³ ( a x )  

H ψ 0 = - ħ 2 a 2 2 m A s e c h a x t g h 2 a x + s e c h 2 a x .

Passo 3

Como sabemos nas identidades trigonométricas, devemos lembrar que:

t g h 2 a x + s e c h 2 a x = s i n h 2 θ c o s h 2 θ + 1 c o s h 2 θ = s i n h ² θ + 1 c o s h 2 θ   =   1

Assim, teremos:

H ψ 0 = - ħ 2 a 2 2 m ψ 0

Portanto, E = - ħ 2 a 2 2 m .

Passo 4

Continuando a equação acima, agora devemos encontrar a integral:

1   =   A 2   ∫ - ∞ ∞ s e c h 2 a x d x   = A 2 1 a   t g h a x ∞ - ∞ = 2 a   A 2

Logo,

A = a 2

A partir disso, teremos o segundo gráfico para a letra b:

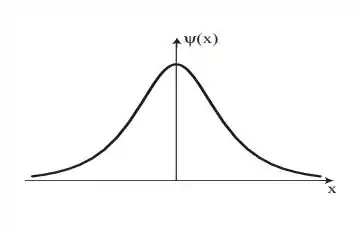
Passo 5

Agora, vamos entender a letra c, que nos pede a demonstração. Nós temos:

d ψ k d x   = A   i k + a   i k   -   a   t g h   a x i k   -   a 2 s e c h 2 a x   e i k x .

d 2 ψ k d x 2 = A   i k + a   i k [ i k - a   t g h   a x i k - a 2 s e c h 2 a x - a 2 i k s e c h 2 a x + 2 a 3 s e c h 2 a x   t g   a x }   e e i k x

Assim, temos que:

- ħ 2 2 m d 2 ψ k d x 2 + V   ψ k = A   i k + a - ħ 2 i k 2 m - k 2 - i a k   t g h   a x - a 2 s e c h 2 a x + ħ 2 a 2 2 m i k s e c h 2 a x - ħ 2 a 3 m s e c h 2 a x   t g h   a x - ħ 2 a 2 m s e c h 2 a x   i k - a   t g h   a x   e e i k x  

Simplificando, nós teremos:

= A e e i k x   i k + a   ħ 2 2 m ( i k 3 - a k 2 t g h   a x + i a 2 k s e c h 2 a x + i a 2 k s e c h 2 a x - 2 a 3 s e c h 2 a x   t g h   a x - 2 i a 2 k   s e c h 2 a x + 2 a 3 s e c h 2 a x   t g h   a x ) .

Assim, temos:

A e e i k x   i k + a   ħ 2 2 m   k ²   i k - a   t g h   a x = ħ 2 k 2 2 m ψ k = E ψ k .

Como x tente ao infinito e a tangente hiperbólica de ax tende a +1, então nós temos:

ψ k ( x ) → A i k - a i k + a e e i k x

E isso representa uma onda transmitida.

Logo, temos que R = 0 ,   T = i k - a i k + a 2 = - i k - a - i k + a i k - a i k + a = 1 .

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro