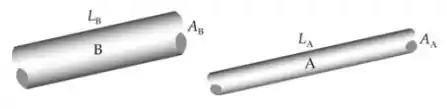
Dois fios cilíndricos de cobre possuem a mesma massa. O fio A tem o dobro do comprimento do fio B. Suas resistências estão relacionadas por (a) . (b) . (c) . (d) .
Passo 1
Olá estudante, vamos responder essa questão passo a passo. Se liga só!
Temos que as resistências dos fios são dadas por , onde é o comprimento do fio e é sua área de seção transversal.
Podemos expressar a razão das resistências e usar a definição de densidade para eliminar as áreas de seção transversal dos fios em favor da razão de seus comprimentos.
Passo 2
Expresse a resistência do fio A:
onde é a resistividade do cobre.
Expresse a resistência do fio B:
Passo 3
Dividindo a primeira equação pela segunda, temos:
ou, como ,
Passo 4
Usando a definição de densidade, expresse a massa do fio A:
Onde é a densidade do cobre.
Expressando a massa do fio B:
Como as massas dos fios são iguais, temos:
ou
Substituindo em , temos:
Assim, temos que a letra (b) está correta.
Resposta
(b) .