Para empurrar um caixote de 25,0 kg numa rampa sem atrito que faz um ângulo de 25° com a horizontal, um operário exerce uma força de 209 N, paralela à rampa. Se o caixote se desloca de 1,5 m, qual o trabalho executado sobre o caixote (a) pelo operário, (b) pelo peso do caixote e (c) pela força normal exercida pela rampa sobre o caixote? (d) Qual o trabalho total executado sobre o caixote?
Passo 1
Fala aí! Antes de começar a resolver questões desse tipo, é sempre bom tentar desenhar o que o enunciado descreve e anotar todas as forças atuantes sobre os corpos, isso vai ajudar bastante na visualização do problema.
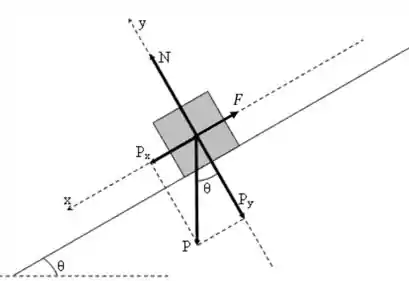
Beleza, agora vamos seguir o passo a passo pra não nos perdermos.
Aquela força ali no desenho, apontando no sentido de subida na rampa, é exercida pelo operário. Se o caixote se desloca nesse sentido, essa força é paralela ao deslocamento, concorda? Olha porque isso é relevante:
Essa equação diz que o trabalho é igual ao produto da força, do deslocamento do corpo e do cosseno do ângulo formado entre as duas variáveis anteriores. Bora aplicar os valores para o primeiro caso:
Passo 2
Agora, o trabalho executado pelo peso do caixote é um pouco mais complicadinho. Isso porque, se você reparar no desenho acima, vai perceber que o peso foi decomposto em , que são suas componentes paralela e perpendicular ao eixo da rampa, respectivamente.
Vamos olhar primeiro para a componente . Para calcular seu módulo, temos que usar as relações trigonométricas do triângulo retângulo. Olha só como fica:
Bora pegar esse valor e calcular o trabalho realizado pela componente x do peso.
Reparou no ângulo ali, né? Usamos pois aponta no sentido oposto ao deslocamento do caixote, ou seja, existem 180° entre esses dois.
Passo 3
Tá, esse foi o trabalho da componente x do peso, mas ainda falta a componente y, né? Cara, dá só mais uma olhada naquele desenho lá e tenta reparar no ângulo que forma com o deslocamento. Reparou? Dá só uma olhada em como fica a expressão do trabalho se formos jogar os valores:
Qual é o cosseno de 90°? Muito bem, é zero! Isso quer dizer que as forças perpendiculares ao movimento do corpo não exercem trabalho. Neste caso, isso vai se aplicar tanto para a componente em y do peso quanto para a força normal!
Resposta
(a) 313,50 J.
(b) -155,31 J.
(c) 0 J.
(d) J.