Uma esfera sólida de peso igual a 35,58 N sobe rolando um plano inclinado, cujo ângulo de inclinação é igual a 30°. Na base do plano, o centro de massa da esfera tem uma velocidade linear de 4,88 m/s. (a) Qual é a energia cinética da esfera na base do plano inclinado? (b) Qual é a distância que a esfera percorre ao subir o plano? (c) A resposta ao item (b) depende do peso da esfera?
Passo 1
Oiiiii gente!
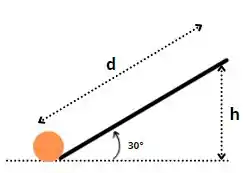
O item (a) da nossa questão deseja saber a energia cinética envolvida nesse rolamento, como sabemos que esse movimento consiste em uma composição de rotação + translação a energia cinética vai ser dada por:
Como e para a esfera temos que , logo a energia cinética terá a forma:
Passo 2
Bom pessoal, excluindo a ação de forças dissipativas, temos que a esfera ao subir a rampa percorre a distância de:
Vimos nesse passo que em nenhum momento utilizamos o peso da esfera para nos auxiliar a encontrar a distância em que a esfera percorre no plano inclinado.
Tudo certinho? Pois bora fazer mais questões!
Bons Estudos!
Resposta
a) K = 60,52 J
b) d = 3,4 m
c) Não depende do peso da esfera