Numa estrada seca, um carro com pneus em bom estado é capaz de frear com uma desaceleração de 4,92 m/s² (suponha constante). (a) Viajando inicialmente a 24,6 m/s, em quanto tempo esse carro consegue parar? (b) Que distância percorre nesse tempo? (c) Faça os gráficos x versus t e v versus t, para a desaceleração.
Passo 1
Fala aí! Essa aqui pede bastante coisa, então vamos seguir um passo de cada vez pra não nos perdermos. Primeiramente, os únicos valores que conhecemos são a velocidade inicial, a final e a aceleração, então temos que procurar uma equação que relaciona esses caras juntamente com o tempo, que é o que nos interessa de fato. Dá só uma olhada nessa aqui:
Essa é a equação horária da velocidade, a qual diz que a velocidade final é igual à velocidade inicial somada da aceleração vezes o tempo. Vamos substituir os valores e ver o que encontramos.
Perceba que trocamos o sinal de + por um de -, pois o movimento se trata de uma frenagem (a aceleração é negativa).
Passo 2
Agora, precisamos encontrar uma equação que nos fornece um meio de encontrar a distância percorrida. Uma alternativa é a função horária do espaço para o movimento uniformemente variado, a qual é expressa assim:
As incógnitas são todas as que já utilizamos anteriormente, com exceção do , que corresponde à distância percorrida. Bora substituir os valores.
Passo 3
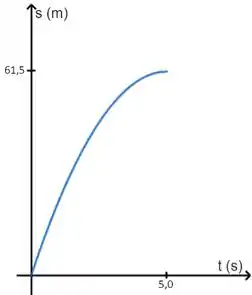
Beleza, agora só nos falta esboçar os gráficos desse movimento. A começar pelo x versus t, temos que procurar uma função que descreva o movimento em termos desses caras. Aquela que usamos no passo anterior é perfeita, concorda? Olha só, podemos reescrevê-la assim:
Se reorganizarmos isso aí, chegamos no seguinte:
Perfeito! Percebe como isso não é nada mais do que uma equação do segundo grau? Esse gráfico nós conhecemos como uma parábola, como só nos interessamos no movimento até a parada completa do veículo, só precisamos esboçar metade dessa parábola. Além disso, repare que o t² acompanha um número negativo, o que já nos permite concluir que a parábola terá concavidade voltada para baixo. Ainda, se substituirmos ali, obteremos como resultado , isso significa que o gráfico parte da origem. Portanto, nosso primeiro esboço vai ficar assim:
Mas dá pra melhorar, né? Podemos marcar alguns valores relevantes aí. Os que mais interessam são os valores em x e em y daquele ponto de máximo ali, que corresponde ao momento de parada.
Aquele ponto máximo é o que chamamos de ponto de inflexão, ele marca o momento em que o corpo, que se movia em um sentido, para e passa a se mover no sentido oposto, ou seja, naquele ponto, a velocidade é zero. No Passo 1, já encontramos que o tempo gasto até que a velocidade se torne nula é 5,0 segundos, então é isso que vamos marcar ali no eixo x.
Similarmente, no passo anterior encontramos a distância percorrida nesse tempo. Portanto, essa será a marcação lá no eixo y. Dá só uma olhada em como vai ficar:

Passo 4
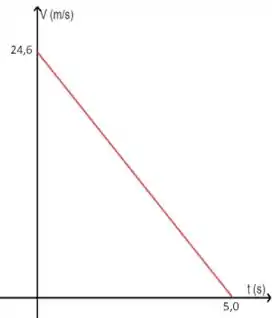
Para finalizar, bora ver como fica o gráfico da velocidade versus tempo. Seguindo o mesmo raciocínio do passo anterior, vamos procurar a melhor função para relacionar esses caras. Aqui, a melhor alternativa é a função horária da velocidade, a mesma que utilizamos lá no Passo 1. Se liga:
Essa é uma equação do primeiro grau, que conhecemos como uma reta, cujo coeficiente angular é negativo, ou seja, é uma reta decrescente. Dessa vez, se substituirmos , vamos obter o coeficiente linear 24,6, que corresponde à altura em que a reta corta o eixo y. O outro ponto importante é aquele em que a reta corta o eixo x, o que também corresponde ao momento em que a velocidade se torna 0. Olha como vai ficar o nosso gráfico:
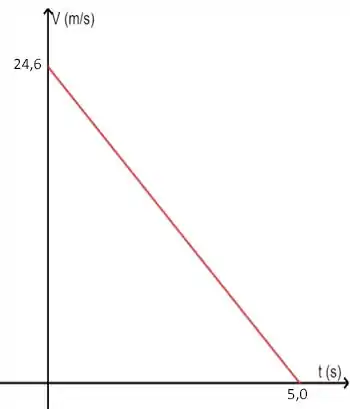
Resposta
(a) 5,0 segundos.
(b) 61,5 metros.
(c)