Na Fig. 33-77, um albatroz está planando horizontalmente com uma velocidade constante de 15 m/s acima de um terreno plano, movendo-se em um plano vertical que inclui o Sol. A ave se aproxima de uma parede de altura h = 2,0 m e está à mesma altura do solo que a extremidade superior da parede. Nessa hora do dia, o ângulo do Sol em relação ao solo é θ = 30°. Com que velocidade a sombra do albatroz se move (a) horizontalmente, ao longo do solo, e (b) verticalmente, ao longo da parede? Mais tarde, um gavião percorre o mesmo caminho, com a mesma velocidade. Você observa que, no momento em que a sombra do gavião atinge a parede, a velocidade da sombra aumenta perceptivelmente. (c) Nesse momento, o Sol está mais alto ou mais baixo no céu que durante o voo do albatroz? (d) Se a velocidade da sombra do gavião na parede é 45 m/s, qual é o ângulo θ do Sol nesse momento?
Passo 1
Opa galerinha, tranquilo? Bora pra uma questãozinha do Halliday.
a) Para descobrir a velocidade em que a sombra do albatroz está se movendo, temos que considerar que o sol está suficientemente distante da terra para que os raios solares sejam considerados paralelos.
Assim, se um raio solar faz um ângulo θ com a horizontal quando o pássaro está em uma posição, outro raio faz o mesmo ângulo quando o pássaro está em outra posição. Com isso podemos concluir que a sombra do albatroz se move na mesma velocidade que o pássaro, ou seja:
Passo 2
Tudo tranquilo até aqui né?...
b) Agora, vamos obter a velocidade do albatroz verticalmente ao longo da parede.
Analisando a figura abaixo, temos:
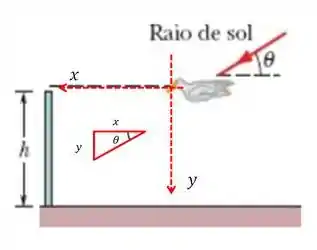
Derivaremos a função em relação à , pois sabemos que tanto o pássaro quanto sua sombra mudam sua posição conforme o tempo.
Sabemos que é a velocidade da sombra do albatroz na horizontal, que pelo item anterior é:
Dado que , temos:
Adotando o eixo y positivo para baixo, significa que a distância y está diminuindo à taxa de
Passo 3
c) Vamos analisar agora a posição do sol durante o voou do albatroz comparando com o do gavião.
No passo anterior descobrimos a relação para o voou dos pássaros, dada por:
Quando o ângulo aumente a partir de , já que o seno está aumentando e o cosseno diminuindo, significa que um valor maior está associado a um valor maior de .
Logo, o sol vai estar mais alto no céu durante o voo do gavião do que durante o voo do albatroz. Já que por sua velocidade na parede da sombra ser maior, o ângulo também será!
Passo 4
d) a mesma formula usada para o albatroz será aplicada para o gavião, assim:
Isolando :
no enunciado temos que a velocidade do gavião na parede é de 45 m/s ou seja , todavia quando a velocidade da sombra do gavião, conforme fala o enunciado, vai ser a mesma do albatroz: .
Assim:
Resposta
Letra a)
Letra b)
Letra c)
O sol vai estar mais alto no céu durante o voo do gavião.
Letra d)