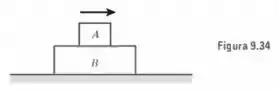
Na Fig. 9.34, as massas dos blocos A e B são m1 e m2. Entre A e B há uma força de atrito de módulo P, mas B pode deslizar sem atrito sobre a superfície horizontal. Inicialmente A está se movendo com velocidade 'V0 enquanto B está em repouso. Se nenhuma outra força agir sobre o sistema, A diminuirá sua velocidade e B acelerar até que os dois blocos se movam com a mesma velocidade v. (a) Que distância A e B se deslocarão antes que isso aconteça, medindo-se essa distância em relação à superfície horizontal? (b) Qual será a variação da energia cinética do sistema em termos da distância de deslocamento de A relativamente a B? (e) O que acontecerá com a quantidade de movimento total?
Passo 1
Faala galera!! Aqui, no instante em que os blocos juntos adquiriram a velocidade v, o bloco A percorreu uma distância x em relação ao ponto 0 e o bloco B uma distância x2 desde o ponto 0. O bloco A terá uma distância x1 em relação a B. Primeiro vamos resolver a questão (c). O momento total é constante porque o sistema está isolado (nenhuma força atua sobre ele), portanto, como o movimento é em linha reta, podemos trabalhar apenas com escalares:
Passo 2
Sabemos também que a mudança na energia cinética é igual ao trabalho realizado pela força de fricção, portanto, para A:
Assim,
Substituindo na equação em que encontramos, temos que:
Passo 3
Portanto, temos que:
Em b, teremos que substituir estes valores encontrados anteriormente e encontrara e energia cinética, dada por:
Resposta
Ei, a resposta está no passo a passo :)