No final da série de óperas de Wagner, O anel dos Nibelungos, Brunhilda tira o anel de ouro do dedo de Siegfried e o arremessa dentro do rio Reno, onde o anel submerge até o fundo. Supondo que o anel fosse pequeno o bastante comparado à profundidade do rio para ser considerado um ponto e que o Reno tenha 10 m de profundidade no ponto em que o anel foi jogado, qual é a área do maior círculo na superfície da água em que a luz do anel poderia escapar da água?
Passo 1
Primeiro de tudo, vamos pensar um pouco: como podemos relacionar o ângulo crítico com a área de uma circunferência?
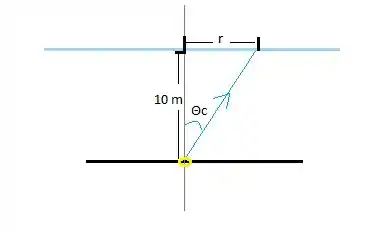
Nesse esqueminha a gente tem o anel lá no fundo do rio a uma profundidade de 10 m. Se a gente aumenta o ângulo para além do ângulo crítico, não tem refração (a luz não muda de um meio para o outro). Então pra isso, a gente tem que estar a uma distância r ali na superfície da água pra que a gente consiga ver essa luz refletida.
Lembrando que .
Passo 2
Beleza, mas e aí? Como a gente vai achar esse e esse ?
O ângulo crítico a gente vai achar pela Lei de Snell.
E esse é o nosso ângulo crítico. Para ângulos maiores que esse, a luz do anel não passa para o ar.
Passo 3
Achando agora aqui a nossa área:
Por trigonometria, temos que . Então:
Calculando então a área, temos: