Uma força de 100 N, fazendo um ângulo acima da horizontal, é aplicada a uma cadeira de 25 kg colocada sobre o chão. (a) Calcule o módulo da força normal que o chão exerce sobre a cadeira e a componente horizontal da força aplicada, para cada um dos seguintes ângulos : (i) 0°, (ii) 30,0°, (iii) 60,0°. (b) Considere que o coeficiente de atrito estático entre o chão e a cadeira é 0,420 e determine, para cada um desses valores de , se a cadeira desliza ou permanece parada.
Passo 1
Fala aí! Pra resolver essa aqui vamos ter que aplicar nossos conhecimentos de decomposição de vetores. Se liga, para cada inclinação da força exercida sobre a cadeira, teremos que decompô-la para encontrarmos suas componentes em x e em y, aí poderemos analisar se a força é suficiente para mover o objeto ou não.
Vamos começar pelo ângulo 0°, que é bem simples. Neste caso, a força de 100 N é paralela ao eixo horizontal, ou seja, só possui uma única componente: a do eixo x.
Agora, para o ângulo de 30,0°, já temos que fazer uma decomposição. A situação que temos é a seguinte:
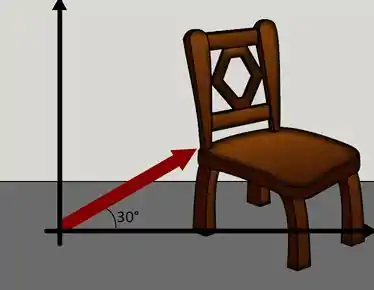
Consegue enxergar o triângulo retângulo formado pelo vetor ali? O cateto oposto ao ângulo de 30° corresponde à componente vertical, enquanto o cateto adjacente corresponde à horizontal. Portanto, basta utilizarmos relações trigonométricas para encontrar cada uma dessas benditas. Se liga:
E para x:
O processo é exatamente o mesmo para o ângulo de 60,0°, basta trocarmos os valores do seno e do cosseno. Como o seno de 60° é igual ao cosseno de 30°, e vice-versa, nem precisamos fazer contas!
Passo 2
Perfeito! Agora, vamos ver o que fazer com todas essas informações.
O enunciado quer que encontremos o módulo da força normal que o chão exerce sobre a cadeira. Isso é muito fácil, é só pegar a massa da cadeira e multiplicar pela gravidade, né?
Bom, não é tão simples assim.
Se liga, acabamos de descobrir que dois dos casos propostos apresentam uma força com componente no eixo y. Não podemos ignorar isso, porque essa componente “anula” parte do peso da cadeira, como se estivesse levantando-a levemente. A ideia, então, é encontrarmos o peso da cadeira e subtrairmos a componente em y de cada força, bora ver como vai ficar:
Como a força aplicada com o ângulo de 0° não tem componente em y, esse é o próprio módulo da força normal.
Passo 3
Para finalizar, vamos analisar se a cadeira desliza ou permanece parada, para cada um desses ângulos. Para que a cadeira deslize, a força horizontal aplicada deve ser maior que a força de atrito estático dessa cadeira, lembrando que ela é dada pelo produto entre seu coeficiente de atrito estático com a superfície e a força normal. Bora ver como fica para cada um dos casos:
Como a força aplicada sobre o ângulo de 0° corresponde a somente 100 N, a cadeira não se move.
Como a componente horizontal da força aplicada sobre o ângulo de 30° vale 86,60 N, ela é suficiente para mover a cadeira.
Novamente, a força aplicada sobre este ângulo não é suficiente para mover a cadeira, pois sua componente horizontal corresponde a 50 N.
Resposta
(a) Para 0°: e
Para 30°: e
Para 60°: e
(b) A cadeira só desliza quando a força é aplicada sobre o ângulo de 30°, quando os ângulos são de 60° ou 0°, ela permanece parada.