A força age sobre um oscilador harmônico que está em repouso em . A massa é , a constante da mola é e . Determine o movimento. Esboce .
Passo 1
Eaew, tudo certinho com você? Bora estudar mais um pouquinho?
Para este problema vamos considerar a equação diferencial de segunda ordem construída utilizando a segunda lei de Newton, com amortecimento, e forçado, saca só!
Precisamos encontrar uma solução para a parte homogênea desta solução, como , note que estou considerando que , temos que este é um amortecimento subcrítico. E a solução da parte homogênea pode ser dada por:
Para encontrar esta solução é necessário utilizar de métodos de equações diferenciais, nós resolvemos isso em outros exercícios deste capítulo do livro, então se não lembrar bem, dá uma checada lá, beleza? Vamos focar em encontrar a solução particular deste sistema!
Passo 2
Temos a seguinte expressão na parte não-homogênea . Como a expressão é composta pela soma de dois termos, teremos que supor duas soluções particulares, e utilizar o método de coeficientes para a soma de chutes, desse jeitinho aqui:
O termo é um polinômio de grau zero e o termo exponencial é o chute devido a parte exponencial de nossa parte não-homogênea. Para usar a equação (1) precisamos das derivadas, vamos fazer isso de uma vez!
Vamos aplicar (4) e (5) na equação (1). Vamo que vamo!
Passo 3
Nós vamos obter o seguinte
Podemos identificar então as equações necessárias para que a igualdade seja possível, e assim determinar nossos coeficientes, saca só!
4
Portanto nossa solução particular (3) toma a forma:
Belezinha, agora só falta aplicar as condições iniciais e cabô! hehehehhe.
Passo 4
A solução geral toma a forma:
O enunciado nos diz que o sistema está em repouso em , e podemos escolher sempre , portanto podemos estabelecer as seguintes condições iniciais:
Vamos precisar também da primeira derivada de (9), vamos fazer isso de uma vez, temos
Beleza, usando (9), (10) e (11) em conjunto, vamos montar um sisteminha linear de equações, bora lá!
Passo 5
Aplicando (10) em (9) temos:
Também temos aplicando (10) em (11):
Nossa solução então fica da forma
O esboço do deslocamento é o seguinte, usando , e :
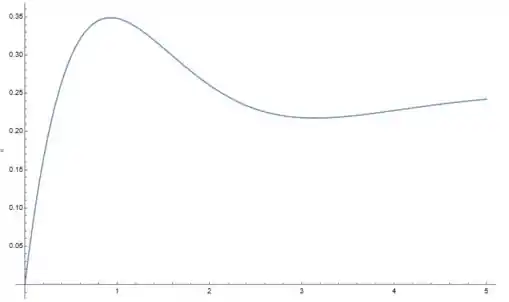
Essa questão foi isso, te vejo na próxima, Tchauzinho!!!