A força de atração entre duas partículas elétricas e separadas por uma distância é
Sendo a permitividade elétrica do meio. A energia potencial correspondente a essa força é
Nesse caso foi escolhida uma distância infinita como o local de energia potencial nula
a) Faça o gráfico de em função da distância entre as duas partículas
b) Suponha que a energia total do sistema considerado seja conhecida. Se e , a que valores de estão limitados os movimentos dessas duas partículas?
c) Qual seria o menor valor de para que as duas partículas pudessem se separar definitivamente?
Passo 1
Salve salveeee, vamos lá!
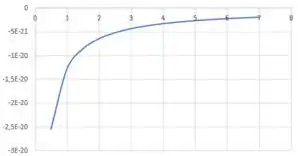
a) Temos que fazer o gráfico de
Para um genérico, o gráfico terá esse formato, onde o eixo horizontal representa e o eixo vertical representa
Passo 2
b) Se , onde é a energia total, temos que a energia cinética (lembrando que )
Como podemos ver no gráfico da letra a, o valor de é negativo para qualquer valor de
Dessa forma, independente da distância , a energia potencial é menor que 0
Passo 3
c) Nesse caso, a distância teria que tender ao infinito, pois é onde a energia potencial é nula
Resposta
a)

b) Qualquer valor de
c)