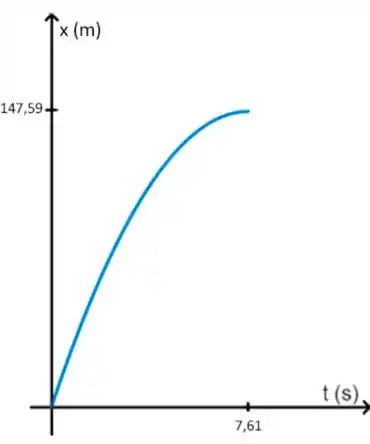
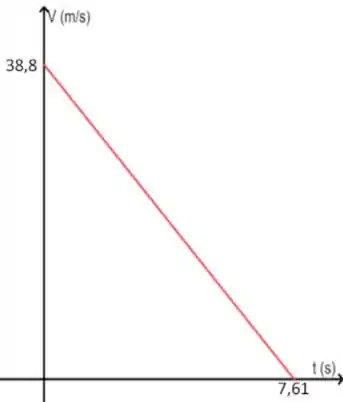
Os freios de um carro são capazes de produzir uma desaceleração de 5,1 m/s². (a) Se você está dirigindo a 140 km/h e avista, de repente, um posto policial, qual o tempo mínimo necessário para reduzir a velocidade até o limite permitido de 80 km/h? (A resposta revela a inutilidade de frear para evitar que a alta velocidade seja detectada pelo radar.) (b) Trace o gráfico x versus t e v versus t para essa desaceleração.
Passo 1
Fala aí! Vamos olhar para o enunciado e ver exatamente as informações que nos foram passadas e o que queremos encontrar: nos foi informado um valor de aceleração, dois de velocidade (uma inicial e outra final) e queremos encontrar o tempo. Então, o que precisamos fazer é encontrar um meio de relacionar esses caras. Dá só uma olhada nessa expressão aqui:
Ela afirma que a aceleração é igual à variação de velocidade dividida pelo tempo, exatamente o que precisamos! Beleza, agora é só substituir os valores e ver o que encontramos. Ah, não podemos nos esquecer de deixar tudo nas mesmas unidades.
Só algumas observações, usamos o valor de para a aceleração pois, como o carro está freando, na verdade ele possui uma desaceleração; além disso, aquele 3,6 aparece ali no lado direito da equação pois esse é o fator de conversão de km/h para m/s.
Passo 2
Beleza, agora só nos falta esboçar os gráficos desse movimento. A começar pelo x versus t, temos que procurar uma função que o descreva em termos da posição em função do tempo. Como estamos diante de um movimento uniformemente variado, vamos olhar para a função horária do espaço, que neste caso é descrita assim:
Aqui, correspondem às posições final e inicial, respectivamente, à velocidade inicial e as demais são as mesmas que utilizamos no passo anterior. Se substituirmos alguns valores e reorganizarmos tudo, vamos chegar no seguinte:
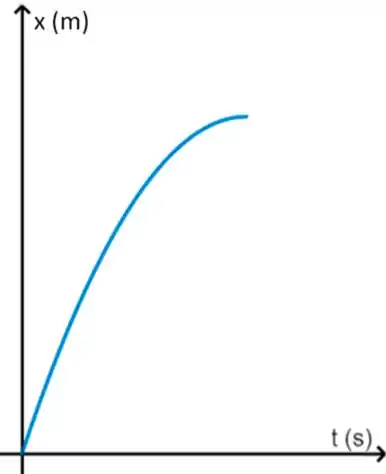
Perfeito! Percebe como isso não é nada mais do que uma equação do segundo grau? Esse gráfico nós conhecemos como uma parábola. Como só nos interessamos no movimento até a parada completa do veículo, só precisamos esboçar metade dessa parábola.
Além disso, repare que o t² acompanha um número negativo, o que já nos permite concluir que a parábola terá concavidade voltada para baixo. Ainda, se substituirmos ali, obteremos como resultado , isso significa que o gráfico parte da origem. Portanto, nosso primeiro esboço vai ficar assim:
Passo 3
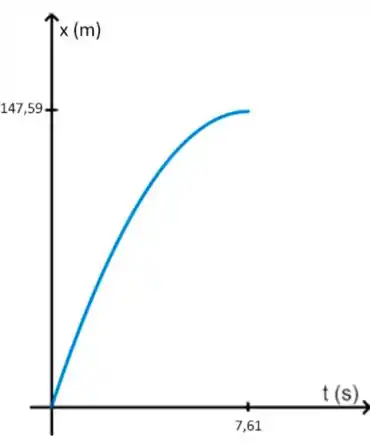
Mas dá pra melhorar, né? Podemos marcar alguns valores relevantes aí. Os que mais interessam são os valores em x e em y daquele ponto de máximo ali, que corresponde ao momento de parada.
Aquele ponto máximo é o que chamamos de ponto de inflexão, ele marca o momento em que o corpo, que se movia em um sentido, para e passa a se mover no sentido oposto, ou seja, naquele ponto, a velocidade é zero. Para encontrarmos em que valor de isso ocorre, vamos utilizar a mesma equação do Passo 1, mas dessa vez com os seguintes valores:
E para encontrarmos o x correspondente, jogamos esse valor na equação do passo anterior:
Beleza, agora podemos anotar esses valores naquele gráfico.
Passo 4
Para finalizar, bora ver como fica o gráfico da velocidade versus tempo. Seguindo o mesmo raciocínio do passo anterior, vamos procurar a melhor função para relacionar esses caras. Aqui, a melhor alternativa é a função horária da velocidade, a mesma que utilizamos lá no Passo 1. Se liga:
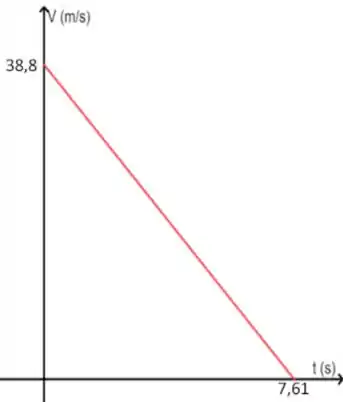
Essa é uma equação do primeiro grau, que conhecemos como uma reta, cujo coeficiente angular é negativo, ou seja, é uma reta decrescente. Dessa vez, se substituirmos , vamos obter o coeficiente linear 38,8, que corresponde à altura em que a reta corta o eixo y. O outro ponto importante é aquele em que a reta corta o eixo x, o que também corresponde ao momento em que a velocidade se torna 0. Olha como vai ficar o nosso gráfico:
Resposta
(a) 3,27 segundos.
(b)