O medo de Bohr para o átomo de hidrogênio pode ser comparado ao sistema Terra Lua, em que o papel da Terra é desempenhado pelo próton e o da Lua pelo elétron, a atração gravitacional sendo substituída pela eletrostática. A distância média entre o elétron e o próton no átomo é da ordem de 0.5 angstrons. (a) Admitindo esse modelo, qual seria a frequência de revolução
do elétron em torno do próton? Compare-a com a frequência da luz visível. (b) Qual seria a velocidade do elétron na sua órbita? É consistente usar a eletrostática nesse caso? É conveniente usar a mecânica não-relativística?
Passo 1
Fala galera, tudo tranquilo? Bem, esse problema consiste em você fazer uma relação entre duas forças conhecidas. Força número 1 é a força eletrostática, a força número 2 é a força centrípeta. O que temos aqui será ilustrado na figura a baixo.
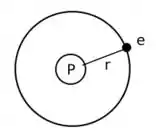
O que nós temos aqui é o próton “P” fazendo o papel da terra e o elétron “e” fazendo o papel da Lua.
O que nós temos agora ṕe uma igualdade entre as forças:
, precisamos relacionar a velocidade linear com a velocidade angular. Já conhecemos bem a relação agora precisamos substituir essa velocidade na nossa equação.
.
As cargas do próton e do elétron são iguais, portanto, temos apenas Q².
Vamos agora relacionar a velocidade angular para que possamos encontrar a frequência. Sabemos que , onde f é a frequência. Substituindo agora essa equação na nossa equação de igualdade das forças, temos
Vamos agora isolar apenas a frequencia.
agora podemos substituir os valores dados no problema se alguns encontrados em tabelas para que possamos chegar em nossa resposta.
Obs:
Passo 2
Para o item (b) nós apenas repetimos alguns passos mas desta vez apenas usando a velocidade linear.
Aplicamos as substituições dos valores e chegaremos em nossa resposta.
Resposta
(a)
Agora, comparando com o espectro da luz visível, que varia entre , nosso resultado é o que podemos afirmar que se encontra na faixa do visível.
(b)
ou .
Um problema deste tipo é mais apropriado de se trabalhar na física quântica. Se trata de um modelo estacionário. Essa velocidade é bem baixa se considerarmos a velocidade da luz. Portanto, não é consistente.