(a) Mostre que existe N! termos na combinação linear de uma autofunção anti-simétrica total que descreve um sistema de N elétrons independentes. (Sugestão: Considere o exemplo 9-2 e utilize a técnica de indução matemática.) (b) Determine o número de tais termos para o caso do argônio com Z = 18. (Sugestão: Use uma tabela matemática para o cálculo de N! ou a fórmula de Stirling, encontrada facilmente em livros de matemática, para aproximar o cálculo.) (c) Estabeleça resumidamente a conexão entre os resultados de (b) e o processo utilizado por Hartree no tratamento do átomo de argônio.

a) para escrever uma autofunção antissimétrica com partículas, usando a notação do determinante:

Isso funciona para uma partícula, agora supomos para partículas, o determinante nos dá Termos, então para a partícula , expandimos o determinante:

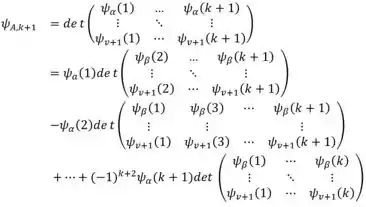
Então assumindo que, cada determinante contribui para Termos, a matriz contribui para Termos para a autofunção completa. Então provamos por indução o que é pedido.

(b) Para o Argônio, temos:

c) Existem grandes números de termos na autofunção. Hartree trata o átomo de argônio usando uma aproximação numérica.