Uma mulher caminha 250 m na direção 30’’ a leste do norte e depois 175 para o leste. (a) Usando métodos gráficos, determine o seu deslocamento resultante a partir do ponto inicial. (b) Compare o módulo do deslocamento com a distância total que a mulher percorreu.
Passo 1
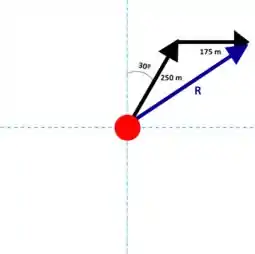
Fala aí! Pra resolver essa aqui, precisamos olhar para os deslocamentos da mulher como vetores. Dá só uma olhada na figura abaixo:
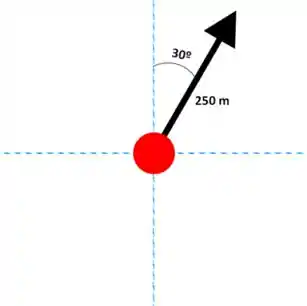
Vamos supor que o círculo vermelho seja o ponto de origem, do qual a mulher parte, as linhas tracejadas sejam os eixos x e y, ou norte-sul e leste-oeste, e a seta seja o primeiro deslocamento 30º a leste do norte. Tudo isso são informações dadas pelo enunciado.
Seguindo as instruções, a próxima etapa é um deslocamento de 175 m para o leste, nosso desenho fica assim:
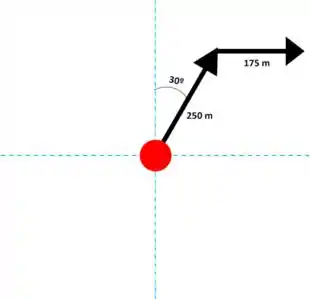
Agora, nos falta encontrarmos graficamente a resultante do deslocamento do ponto de origem até o final. Tá lembrado como fazemos isso?
Um dos métodos possíveis é a regra do polígono. Esse cara nos diz que, para somarmos vetores graficamente, juntamos os vetores pela extremidade do primeiro e origem do segundo e traçamos uma linha da origem do primeiro para a extremidade do último vetor, essa linha será a resultante. No nosso desenho, a resultante será aquela linha que surge ali embaixo:
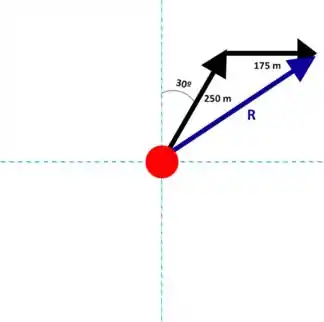
Passo 2
Beleza, agora precisamos comparar o módulo desse vetor deslocamento resultante para compará-lo com a distância total percorrida. Para fazer isso, precisamos utilizar a lei dos cossenos, que é expressa assim:
Ali, é o ângulo formado entre os vetores e , que seria aquele ângulo interno oposto ao lado R na figura acima. Aí complicou, né, pois não sabemos o valor desse ângulo, e agora? Caaalma, meu jovem, que já vamos dar um jeito.
Olha só, se prolongarmos a reta daquele deslocamento de cima, vai aparecer o seguinte:
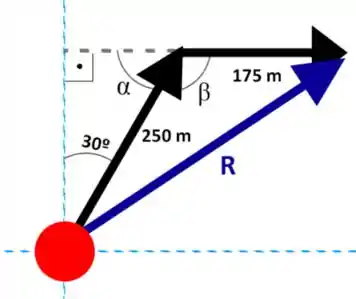
Perceba que o vetor forma um ângulo reto com o eixo y. Isso, somado ao fato de que os ângulos internos a um triângulo sempre devem somar 180º, nos permite concluir que aquele ângulo alfa que faltava naquele triângulo que surgiu ali vale:
Beleza, agora a gente consegue descobrir o ângulo que nos interessa de fato, concorda? Eu marquei ele como na figura acima. Perceba que ele e o que encontramos logo há pouco são ângulos suplementares, ou seja, eles devem somar para . Com isso, podemos finalmente concluir que esse danado vale .
E agora aplicamos todos os valores conhecidos na lei dos cossenos. Ficamos assim:
Este é o valor do módulo do deslocamento, o qual é bem menor do que a distância de 425 m percorrida pela mulher!
Resposta
(a)
(b) O módulo do deslocamento é 222,20 m e é menor que a distância total percorrida.