Um múon (uma partícula elementar) entra num campo elétrico com uma velocidade de m/s, onde é desacelerado à razão de m/s². (a) Que distância o múon percorre até parar? (b) Faça os gráficos x versus t e v versus t para o múon.
Passo 1
Fala aí! Pra resolver a primeira parte dessa aqui vamos ter que aplicar a equação de Torricelli, pois nos foram informadas a velocidade e a aceleração, e precisamos encontrar a distância percorrida:
Esse cara nos diz que o quadrado da velocidade final é igual ao quadrado da velocidade inicial somado do dobro da aceleração vezes a distância percorrida. Bora substituir os valores e resolver isso aí.
Preste bem atenção em qual é a velocidade inicial e qual é a final, além disso, a aceleração é negativa pois a partícula está parando. Vamos resolver para :
Passo 2
Beleza, agora, para podermos desenhar os gráficos em função do tempo, vamos relembrar mais duas funçõezinhas bem conhecidas do movimento uniformemente variado. A primeira delas é a função horária do espaço e é expressa assim:
Se substituirmos alguns valores conhecidos, ficamos assim:
Deixa eu reorganizar isso aí pra ficar mais fácil de perceber uma coisa.
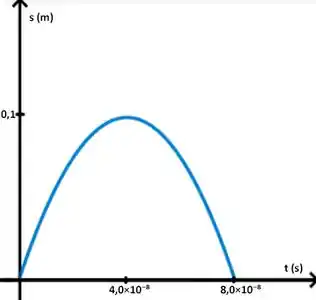
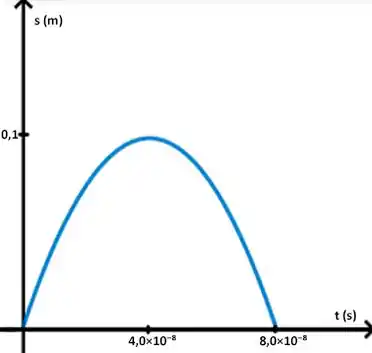
Bom, o que eu quero que você perceba é que isso nada mais é do que uma equação do segundo grau, cujo gráfico conhecemos como uma parábola. Repare que o t² acompanha um número negativo, o que já nos permite concluir que a parábola terá concavidade voltada para baixo. Além disso, se substituirmos ali, obteremos como resultado , isso significa que o gráfico parte da origem. Portanto, nosso primeiro esboço vai ficar assim:
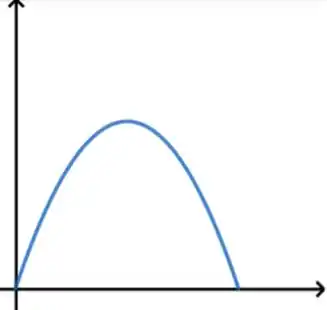
Mas dá pra melhorar, né? Podemos marcar alguns valores relevantes aí. Os que mais interessam são o valor em x e em y daquele ponto de máximo, e o ponto que encontra o eixo x lá no final.
Um desses caras já conhecemos. Aquele ponto máximo é o que chamamos de ponto de inflexão, ele marca o momento em que a partícula, que se movia em um sentido, para e passa a se mover no sentido oposto, ou seja, naquele ponto, a velocidade é zero. No passo anterior, já encontramos que o espaço percorrido até que a velocidade se torne nula é 0,1 m, então é isso que vamos marcar ali no eixo y.
Agora, para encontrarmos o tempo correspondente a esse espaço, temos algumas alternativas. Poderíamos substituir lá na função horária do espaço, mas daria um pouquinho de trabalho. Vou introduzir mais uma equação aqui, pois acredito que será mais fácil:
Essa é a função horária da velocidade, a qual diz que a velocidade final é igual à velocidade inicial somada da aceleração vezes o tempo. Assim, podemos jogar e resolver facilmente para t, se liga:
Beleza, agora falta somente aquele último ponto. Para não precisarmos fazer nenhuma conta adicional, repare em uma coisa: como o gráfico dessa função é simétrico, esse ponto de máximo que encontrarmos o divide ao meio, ou seja, o ponto que nos falta tem valor em x igual ao dobro desse valor que acabamos de calcular.
Agora sim, bora colocar todos esses valores no gráfico pra ficar tudo certinho.
Passo 3
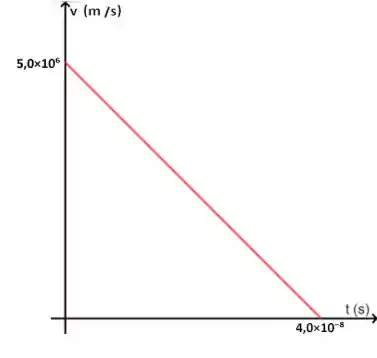
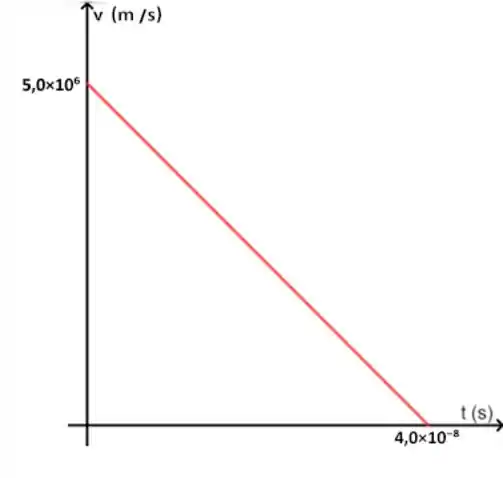
Beleza, para finalizar, nos falta somente o gráfico da . Se você tiver se ligado no que fizemos anteriormente, deve ter percebido que já usamos uma função que vai cair muito bem aqui: a função horária da velocidade.
No passo anterior, utilizamos o seguinte:
Utilizando o mesmo raciocínio do passo anterior, podemos perceber que dessa vez se trata de uma função do primeiro grau, ou seja, o gráfico é representado por uma reta. Como o termo que acompanha a variável é negativo, trata-se de uma reta decrescente. Ainda, se jogarmos nessa equação, podemos perceber que o que sobra é , ou seja, a velocidade inicial. E quando que a velocidade se torna zero? Ora, no tempo que já encontramos anteriormente.
Então, nosso gráfico vai ficar assim:
Resposta
(a) 0,1 metros.
(b)