Um objeto pontual está a 10 cm de distância de um espelho plano, e o olho de um observador (cuja pupila tem 5,0 mm de diâmetro) está a 20 cm de distância. Supondo que o olho e o objeto estão na mesma reta perpendicular à superfície do espelho, determine a área do espelho envolvida na observação do reflexo do ponto.
Passo 1
Opaa, tranquilo? Vamos para mais uma questão de formação de imagens em espelhos planos.
A figura abaixo exemplifica o que está acontecendo no problema.
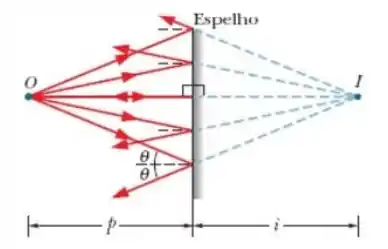
Note que em cada lado existem dois raios que chamaremos de e , que estão localizados acima e abaixo do raio normal. Os dois raios têm também o mesmo ângulo de incidência θ.
Iremos supor que os dois raios atingem a extremidade superior e a extremidade inferior da pupila depois de seres refletidos. Se atinge o espelho no ponto A e o raio atinge o espelho no ponto B, a distância entre A e B é dada por:
Onde é a distância do espelho ao objeto.
Passo 2
Note que podemos construir um triângulo tomando como um dos vértices a imagem do objeto (o ponto da imagem do passo 1), situado a uma distância atrás do espelho.
Um cateto do triângulo coincide com o raio normal (que liga o ponto ao centro da pupila), e a hipotenusa coincide com o raio r (depois de refletido). E a distância entre a pupila e o olho é dada pela seguinte relação , onde o menor ângulo do triangulo é dado por θ!
Onde é o raio da pupila que pelo enunciado vale . Assim, juntando com a formula anterior temos:
Substituindo os valores:
Passo 3
Calmaaa que ainda não acabou!
O valor de é o diâmetro de uma área circular A do espelho tal que todos os raios refletidos em pontos dessa área chegam ao olho. Assim, a área abrangida será de: