Um operário empurrou um bloco de 27 kg por uma distância de 9,2 m num piso plano, com velocidade constante, aplicando uma força dirigida 32° abaixo da horizontal. Se o coeficiente de atrito dinâmico é 0,20, qual o trabalho executado pelo operário sobre o bloco?
Passo 1
Fala aí! Antes de começar a resolver questões desse tipo, é sempre bom tentar desenhar o que o enunciado descreve e anotar todas as forças atuantes sobre os corpos, isso vai ajudar bastante na visualização do problema.
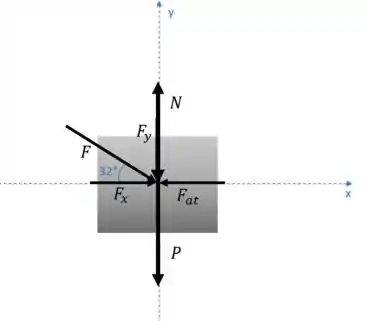
Beleza, anotei ali: a força de atrito , o peso (P), a normal (N) e a força exercida pelo operário . Já aproveitei para decompor essa força em suas componentes em x e y também.
Para encontrarmos o trabalho realizado pelo operário, vamos usar a seguinte expressão:
Essa expressão diz que o trabalho é igual ao produto entre a força, o deslocamento e o cosseno do ângulo entre essas duas variáveis anteriores. O problema é que, de início, não conhecemos a força , então, temos que procurar um jeito de encontrá-la.
Nossa solução pode vir por meio da segunda lei de Newton:
Essa expressão afirma que a força resultante é igual ao produto da massa e da aceleração. E qual é a força resultante aqui? Bom, se olharmos para o eixo x, veremos que as únicas forças atuantes são no sentido positivo e no sentido contrário ao movimento, ou negativo.
Ainda, o enunciado nos informou que o bloco desliza com uma velocidade constante, isto é, sua aceleração é igual a zero. Portanto:
Passo 2
A força de atrito nós conseguimos encontrar, né?
O coeficiente de atrito nos foi fornecido pelo enunciado, e a normal sabemos calcular facilmente. Logo:
E, como vimos no final do passo anterior, esse também é o valor da componente x da força F.
Passo 3
Perfeito! Agora que temos o valor de , podemos olhar para aquele triângulo retângulo formado pelas componentes de e usar as relações trigonométricas para descobrir o valor de . Se liga:
Passo 4
Finalmente, podemos calcular o trabalho exercido pelo operário. A partir daquela equação introduzida lá no início do Passo 1, vamos substituir os valores encontrados.
Resposta
485,76 J.