Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alonso e Finn - Mecânica- Ed: 2º - Capítulo 10.Problemas - Ex. 44

Uma partícula de massa m move-se ao redor de um eixo com uma velocidade angular w tal que sua velocidade é v = w x r, ele acordo com a Eq. (5.48). Prove que as componentes cio seu momento angular são

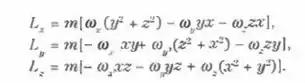
Passo 1

Faala galera!! Aqui, teremos que relembrar algumas equações importantes:

r = x i + y j + z k

w = x x i + w y j + w z k

I = r   X   p = m r   X   v

aqui, realizando os produtos vetoriais e substituições, conseguimos chegar em:

I = m [ ( x ² + y ² + z ² ) ( w x i + w y j + w z k ) - ( x w x + y w y + z w z ) ( x i + y j + z k ) ]

Colocando na forma das componentes i, j e k, teremos:

I = [ m x ( x ² + y ² + z ² ) - x ( x w x + y w y + z w z ) ] i + [ m y ( x ² + y ² + z ² ) - y ( x w x + y w y + z w z ) ] j + [ m z ( x ² + y ² + z ² ) - z ( x w x + y w y + z w z ) ] k

Passo 2

Assim, vemos que, em cada colchete, conseguimos eliminar os termos de x²wx, y²wy…, tendo:

P r i m e i r o   c o l c h e t e :   L x = m [ w x ( y ² + z ² ) - w y y z + w z z x ]

S e g u n d o   c o l c h e t e :   L y = m [ w y ( x ² + z ² ) - w x x y - w z z y ]

T e r c e i r o   c o l c h e t e :   L z = m [ w z ( y ² + x ² ) - w x x z - w y y x ]

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro