A posição de um elétron é dada por (onde t está em segundos e as unidades dos coeficientes são tais que r está em metros). (a) Qual é v(t) para o elétron? (b) Na notação de vetores unitários, qual é v em t = 2,0 s? (c) Quais são o módulo e a direção de v, logo depois?
Passo 1
Fala aí! Para resolver essa aqui, vamos ter que resgatar um conceito bem importante: o vetor velocidade pode ser encontrado pela derivada da posição em relação ao tempo.
Para resolver isso, basta derivarmos cada termo da função individualmente, aí chegaremos no seguinte:
Passo 2
Beleza, para encontrar a velocidade em t = 2,0, é só substituirmos o valor na função que encontramos anteriormente. Se liga:
E para encontrarmos o módulo desse cara, vamos fazer a raiz quadrada da soma das componentes ao quadrado. Olha só:
Passo 3
Pra finalizar, vamos encontrar um meio de expressar a direção desse cara. Se olharmos pra esse vetor velocidade, perceberemos que ele tem uma componente -16 em y e 3 em x, assim, podemos desenhar um triângulo retângulo cujos catetos valem 16 e 3 e a hipotenusa vale 16,3.
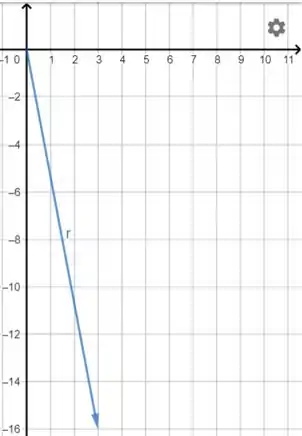
O ângulo oposto ao cateto maior é o ângulo que o vetor velocidade faz com a horizontal. Então, vamos calculá-lo assim:
Como se trata da tangente, isso nos retorna dois resultados:
Qual deles iremos escolher? Ora, o ângulo de 101° se encontra ali no segundo quadrante, logo após o de 90°, enquanto o de -79,4° se encontra lá no quarto, exatamente onde precisamos. Portanto, o vetor velocidade forma um ângulo de -79,4° com a horizontal.
Resposta
(a)
(b)
(c) na direção com um ângulo de -79,4° com a horizontal.