Referindo-se aos Probs. e , suponha que e que . (a) Determine a excentricidade da órbita do projétil. (b) Escreva a equação da órbita. (c) Prove que o projétil cairá, de retorno à Terra, num ponto a uma distância de igual a , medida ao longo da superfície da Terra. Faça, num papel de gráfico polar, um gráfico da trajetória do projétil. [Sugestão: após calcular , determine os valores de para os quais . Um dos valores corresponde ao ponto de lançamento e o outro ao ponto de retorno. A diferença entre os dois ângulos dá o deslocamento angular.]
Passo 1
E aí, beleza?? Aplicando a equação demonstrada no problema , temos:
Passo 2
Aplicando a equação demonstrada no problema , temos:
Passo 3
Para o ponto de retorno, temos que , logo:
Ou seja:
Logo, a separação angular é:
E a distância entre os pontos é:
Passo 4
A trajetória é a seguinte:
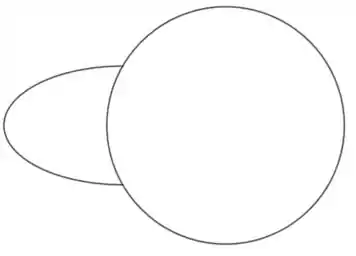
Em que a circunferência é a Terra, enquanto o arco de elipse representa a trajetória do projétil.
Resposta
Ei, a resposta está no passo a passo :)