Resolva o Probl. 39 para o caso em que a massa sofre um deslocamento inicial e uma velocidade inicial orientada na direção do ponto de equilíbrio. Mostre que se , a massa ultrapassará a posição de equilíbrio, nos casos de amortecimento crítico e superamortecimento, de modo que os comentários feitos no final da Seç. 2.9 não se aplicam a este caso. Esboce os movimentos para este caso.
Passo 1
Eaew, belezinha? Vamos começar mais um belo dia de estudos?
Primeiro, que problema é esse, o tal de 39? O enunciado do mesmo é o seguinte:
“Uma massa submetida a uma força restauradora linear e a um amortecimento desloca-se a uma distância da posição de equilíbrio, sendo largada com velocidade inicial igual a 0. Determine os movimentos para os casos de subamortecimento, amortecimento crítico e superamortecimento.”
Antes de qualquer coisa vamos analisar o diagrama de forças relacionado a esse sistema e montar a equação diferencial relacionada, belezinha?
Passo 2
Temos o seguinte diagrama de forças para este sistema:
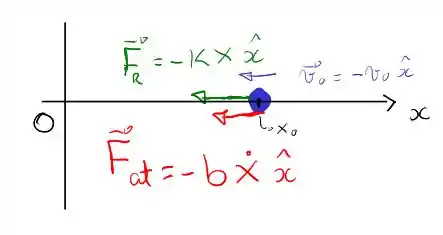
Se utilizarmos a Lei de Newton, podemos montar a seguinte equação diferencial de segunda ordem:
Em que , estou ignorando os versores pois este é um movimento unidimensional, apenas para a conta ficar menos poluída, mas tome cuidado com o sinal ao utilizar a segunda lei de newton. Reescrevendo um pouco esta equação, obtemos o seguinte sistema:
Belezinha, agora vamos analisar a resolução desta equação diferencial.
Passo 3
Essa equação em particular é uma equação diferencial ordinária de segunda ordem homogênea, portanto, podemos resolvê-la e obter uma solução única contanto que tenhamos 2 condições iniciais. As nossas condições neste problema são:
e
Para resolver nossa equação diferencial, no entanto é necessário aplicar algumas técnicas, saca só!
Passo 4
De cara já vamos escrever o nosso polinômio característico, da seguinte maneira:
O polinômio é composto de maneira que o coeficiente do termo com derivada segunda multiplica um termo de , o coeficiente da primeira derivada um termo do tipo e o termo sem derivada nenhuma, um termo do tipo . Para propor uma solução para nossa EDO, precisamos saber as raízes deste polinômio, elas são da forma:
Aqui eu simplesmente apliquei Bhaskara, e também que que e . Note que dependendo do valor da raiz, isso nos dará uma solução diferente, é aí que estaremos determinando o nosso sistema como subcrítico, supercrítico ou crítico. Vamos fazer isso!
Passo 5
O sistema está em um amortecimento subcrítico se , ou seja, nossas raízes tomam a forma:
Em que Beleza, com isso podemos escrever a nossa primeira solução! Bora lá!
Passo 6
A solução de uma equação diferencial com raízes complexas distintas é da forma:
ou seja:
Agora precisamos aplicar as condições iniciais, bora lá!
Passo 7
A primeira condição é , portanto:
e a segunda condição é da forma , portanto:
de forma que:
Isso nos dá um sistema de equações lineares para resolver, vamos fazer isso então!
Passo 8
Podemos utilizar diretamente a equação 9 dentro da equação 10 para obter:
Usando este resultado na equação 9, temos:
E para temos utilizando a equação 11, que:
Com a equação 11 e 12 em mãos podemos escrever a nossa solução! Bora lá!
Passo 9
Para o caso subcrítico temos a seguinte solução para este sistema:
Utilizando a identidade , temos:
E esta é a nossa resposta para o amortecimento subcrítico, bora para o caso supercrítico!
Passo 10
O sistema está em um amortecimento subcrítico se , ou seja, nossas raízes tomam a forma:
Ou seja, raízes reais e distintas. Utilizando o mesmo formato de anteriormente para a solução da nossa equação diferencial, temos:
Em que e . Precisamos aplicar as condições iniciais novamente!
Passo 11
A primeira condição é , portanto:
e a segunda condição é da forma , portanto:
de forma que:
Isso nos dá um sistema de equações lineares para resolver, vamos fazer isso então!
Passo 12
Podemos utilizar diretamente a equação 17 dentro da equação 18 para obter:
Usando este resultado na equação 17, temos:
Tendo as equações 19 e 20 em mãos podemos escrever nossa solução para o caso supercrítico, saca só!
Passo 13
Para o caso supercrítico temos a seguinte solução para este sistema:
Essa é a nossa solução para o caso supercrítico! Falta só um agora, o caso crítico, aguenta firme aí!
Passo 14
O sistema está em um amortecimento crítico se , ou seja, nossas raízes tomam a forma:
Ou seja, raízes iguais, agora diferentemente do que fizemos antes temos que tomar um certo cuidado com as nossas soluções, elas irão tomar o seguinte formato para garantir a independência linear de ambas as componentes:
Precisamos aplicar as condições iniciais novamente!
Passo 15
A primeira condição é , portanto:
e a segunda condição é da forma , portanto:
de forma que:
Podemos utilizar diretamente a equação 23 dentro da equação 24 para obter:
Tendo as equações 24 e 25 em mãos podemos escrever nossa solução para o caso crítico, saca só!
Passo 16
Para o caso crítico temos a seguinte solução para este sistema:
Essa é a nossa solução para o caso crítico! Vamos agora analisar o que acontece se temos , e ver se isso realmente faz a massa ultrapassar o ponto de equilíbrio. Bora lá!
Passo 17
No caso do superamortecimento temos a seguinte solução:
Devido ao que se pede, é interessante analisar o balanço de energia deste sistema, ou seja:
O sistema passa pelo ponto de equilíbrio quando a energia potencial é nula, ela ultrapassará tal ponto se ainda houver energia cinética no instante de tempo em que a alcança. Vamos verificar isso!!
Passo 18
Quando , temos:
Utilizando esta relação na relação para a velocidade, temos:
Se utilizarmos a equação 26 nesta expressão obtemos:
Ou seja, a velocidade só é nula se , se temos a relação pedida, ele necessariamente terá um movimento quando chegar ao ponto de equilíbrio. Vamos analisar agora o caso do amortecimento crítico, beleza?
Passo 19
No amortecimento crítico temos que , e portanto, , de maneira que nossa relação para a velocidade se torna . Todo o resto do processo é análogo, saca só! A solução é da forma:
No equilíbrio temos:
Calculando a derivada, nós temos:
Aplicando condição 28, temos:
Essa relação só se anula quando temos , ou seja, temos que com a relação suposta, ainda há velocidade nesta partícula. Vamos fazer alguns plots finais como esboço, e acabou… Uff…
Passo 20
Vou dar valores arbitrários para algumas constantes, de forma que o plot fique mais simples, no caso, colocarei , (subcrítico e crítico) e , com (supercrítico, para este caso será usado ), (crítico) e (subcrítico), belezinha? O plot fica da seguinte maneira:
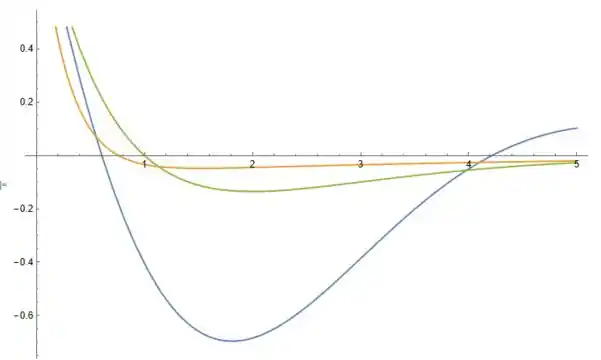
A curva azul é relativa ao amortecimento subcrítico, a curva verde ao crítico e a curva laranja ao supercrítico. Uff… A questão foi isso, te vejo na próxima! Tchauzinho!
Resposta
Ao longo dos passos.