Um trem se move para o leste com uma velocidade constante de 60,0 km/h, durante 40,0 min, depois, na direção 50,0º nordeste, durante 20,0 min e, finalmente, na direção oeste, durante 50,0 min. Qual a velocidade média do trem durante esse percurso?
Passo 1
Fala aí! Se desenharmos o percurso realizado pelo trem, conforme as instruções fornecidas pelo enunciado, vamos chegar em algo mais ou menos assim:
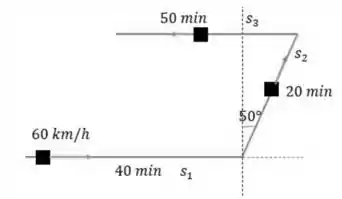
Para encontrarmos a velocidade vetorial média, precisamos encontrar o vetor deslocamento. Bora ver como fica isso, então.
O vetor deslocamento tem componentes iguais à soma das componentes de cada um dos vetores do percurso. As componentes de conseguimos encontrar logo de cara, né?
Só algumas observações: fazemos pois queremos encontrar a distância percorrida pelo trem a uma velocidade de 60 km/h em um intervalo de 40 min. Ali em , usamos -60 pois o trem se move no sentido oposto ao nosso referencial positivo, tranquilo?
Beleza, agora para o . Vamos ter que fazer uma decomposição para encontrar suas componentes em x e em y:
Passo 2
Agora sim, podemos somar todas essas componentes:
Pela definição do módulo de vetor, podemos fazer:
Passo 3
Com esse dado em mãos, podemos, finalmente, encontrar a velocidade vetorial média. Para isso, vamos dividir esse valor encontrado pelo tempo total gasto para percorrer o percurso. O tempo total é:
E isso equivale a 1,83 horas. Portanto:
Resposta
A velocidade vetorial média é de 7,61 km/h e tem direção do vetor deslocamento.