Um bloco de alumínio de massa e um bloco de cobre de massa estão conectados por uma corda leve sobre uma polia sem atrito. Eles estão sobre uma superfície de aço como mostrado na Figura P5.46, onde .
- Quando são liberados do repouso, eles se moverão? Se assim fizerem, determine
- sua aceleração e
- a tensão na corda. Se eles não se moverem, determine
- a soma dos módulos das forças de atrito que agem nos blocos.
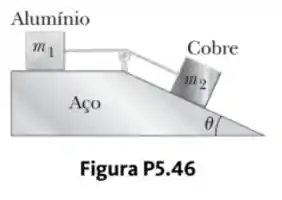
Passo 1
E aiii gente, tudo bom com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo e bora!
Letra a:
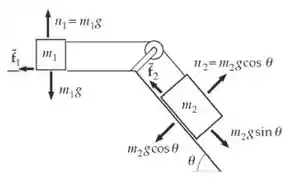
Para o sistema começar a se mover quando liberado, a força que tende a mover para baixo na inclinação, , deve exceder a força de atrito máximo que pode retardar o movimento:
Da tabela de coeficientes de atrito no livro, usamos
Com , a força de atrito máxima é . Esta, excede a força que tende a fazer com que o sistema se mova,
Então, o sistema não começará a se mover quando liberado.
Passo 2
Letra b e c:
Sem resposta porque os blocos não se movem.
Passo 3
Letra d:
As forças de atrito aumentam em magnitude até o atrito total que retarda o movimento, ser igual à força que tende a colocar o sistema em movimento. Ou seja, até:
Resposta
- Sem resposta porque os blocos não se movem.
- Sem resposta porque os blocos não se movem.