Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 10.Problemas fundamentais - Ex. 4
Determine o momento de inércia da área sombreada em relação o eixo .
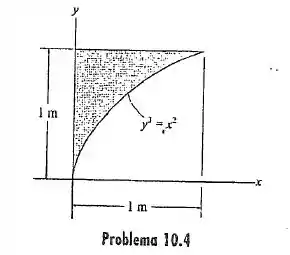
Passo 1
Falaa! Ele quer o momento de inércia da área em relação a A fórmula do momento de inércia em relação ao eixo é
O que a gente precisa fazer é motar essa integral. Vem ver como!
Nós precisamos escolher um retângulo bem fininho paralelo a que esteja contido na nossa área, que chamamos de elemento infinitesimal de área. A carinha dele:
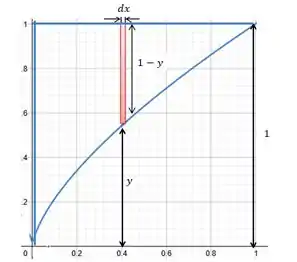
Repara que a altura dele é a diferença entre a altura total da nossa área que vale 1 e , que é altura do ponto onde nosso retângulo começa.
Então nosso elemento tem altura e largura . Por isso o elemento infinitesimal de área vai ser igual a
Como ali a gente tem um , precisamos colocar todo em função de . Precisamos então de em função de . Lembra que ele nos deu uma função que representa essa curva azul:
Então
Passo 2
Agora é só reolver a integral
Quem vão ser os extremos de integração? Vai ser o intervalo de que contém nossa área, já que temos na integral. Percebe que esse intervalo é
Então: