Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 47
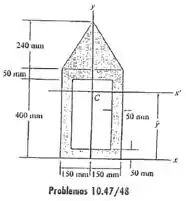
10.46 Determine o momento de inércia da área composta em relação ao eixo centroidal .
Passo 1
Vamos separar essa área desse jeito:
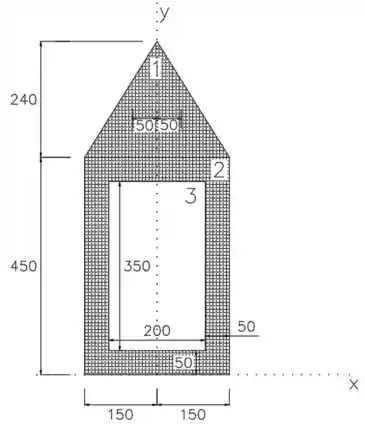
O momento de inércia total será a soma dos momentos de inercia dos triângulos 1 e do retângulo 2, menos o momento de inercia do retângulo 3.
Pela tabela, sabemos que o momento de inércia de um triângulo é igual a , podemos observar que os dois triângulos estão em lados opostos do eixo e tem o mesmo tamanho e distância do eixo até seu centroide, precisamos usar o teorema dos eixos paralelos. Então o momento de inercia dos dois triângulos 1 é:
Também pela tabela, nós sabemos que o momento de inercia de um retângulo é igual a , não precisamos utilizar o teorema dos eixos paralelos para nenhum dos dois retângulos, pois seus centroides coincidem com o eixo , então o momento de inercia ira ficar:
e
Passo 2
A área da base e a altura dos retângulos e do triângulo o exercícios nos dá. A distância até o centroide de cada triângulo é facinho de calcular, assim como sua área:
A área vai ser:
Vamos calcualr os três momentos de inercia e então soma-los:
Triângulos 1:
Para os retângulos é legal reparar que seus centroides já estão alinhados com o eixo , portanto, não é necessário aplicar o teorema dos eixos paralelos.
Retângulo 2:
Retângulo 3:
Então, somando os três valores, vamos obter: