Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 6.3 - Ex. 12
12- Determine a força em cada elemento da treliça e indique se esses elementos estão sob tração ou compressão. Considere que e .
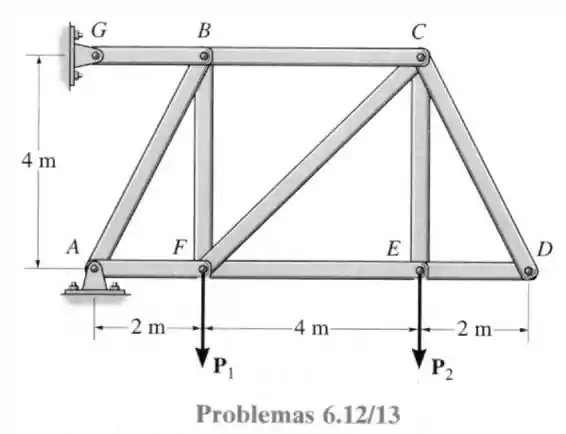
Passo 1
As duas reações tem capacidade de resistir na vertical e na horizontal só que o apoio só tem uma força na horizontal pois só a barra imprime esse esforço, então temos as seguintes reações nos apoios.
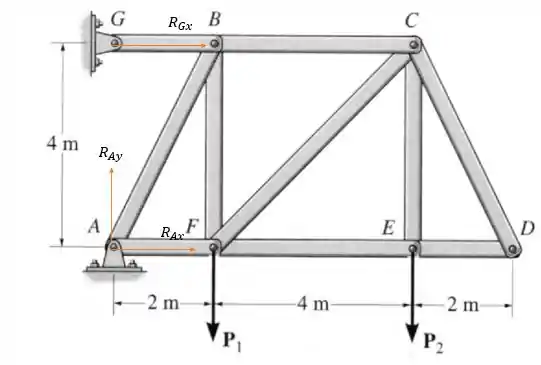
Como e temos que pela somatória das forças verticais:
E pela somatória dos momentos em :
Isso quer dizer o sentido dessa força está ao contrário da que foi desenhada.
E pela somatória das forças horizontais que:
Passo 2
Vamos agora analisar o nó :
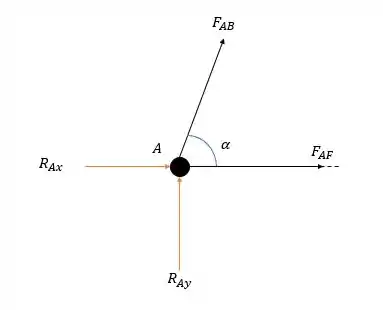
Fazendo a somatória das forças verticais temos:
Onde vale:
Substituindo os valores que conhecemos temos:
Força compressiva.
E pela somatória das forças horizontais:
Força compressiva também.
Passo 3
Vamos passar rapidinho pelo nó .
Pela somatória das forças horizontais temos:
Isso torna melhor a visualização das forças no nó .
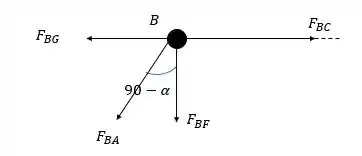
Pela somatória das forças verticais temos:
Agora fazendo a somatória das forças horizontais:
Passo 4
Agora vamos para o nó :
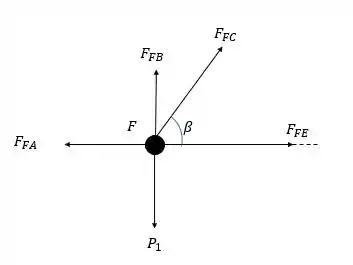
Fazendo a somatória das forças verticais:
Onde vale:
Logo:
Força compressiva.
Agora fazendo a somatória das forças horizontais:
Passo 5
Agora vamos para o nó :
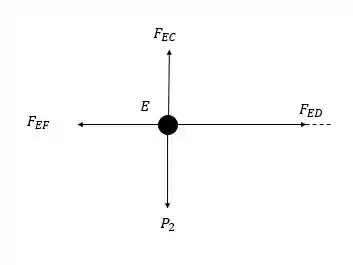
Pela somatória das forças verticais:
E a somatória das forças horizontais:
Agora para o nó :
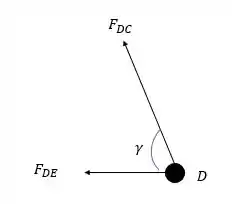
Onde vale:
E pela somatória das forças horizontais temos: