Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 5.Revisão - Ex. 99
99- Determine os componentes de reação na parede fixa . A força de é paralela ao eixo e a força de é paralela ao eixo .
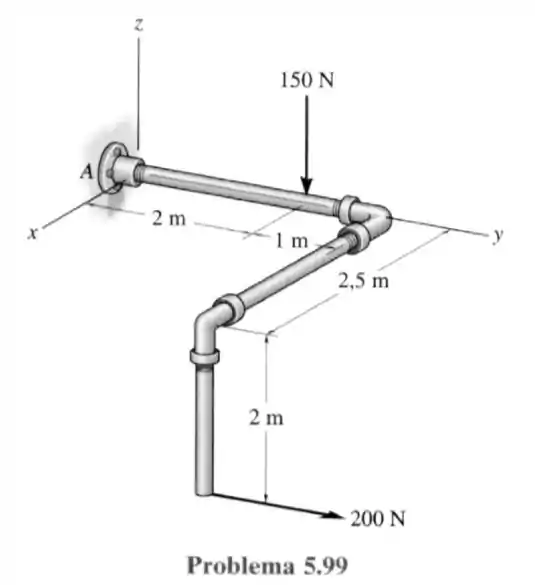
Passo 1
Desenhando as forças e momentos que a junta oferece ao sistema nós teremos (forças positiva e momentos no sentido anti-horário).
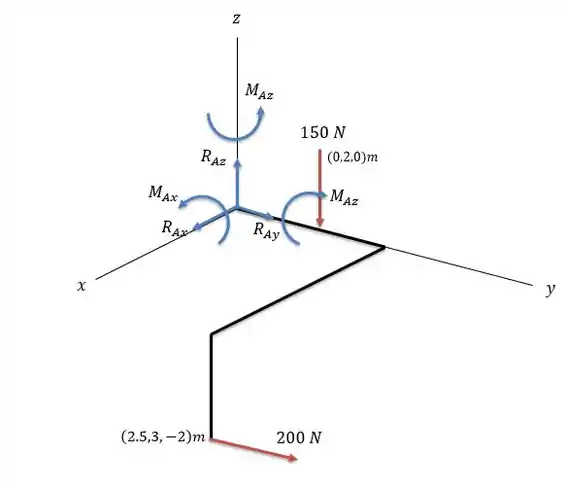
Passo 2
Fazendo a somatória das forças em temos:
A somatória das forças temos:
E a somatória das forças em :
Passo 3
Agora vamos calcular os momentos:
Para calcular os momentos em temos que identificar as forças em com as distância em e as forças em com as distâncias em . Logo:
Onde a forma trata o sentido anti-horário como positivo.
Agora para encontrar o momento em temos que pegar as forças em com distância e as forças em com as distâncias em .
Agora para encontrar o momento em temos que pegar as forças em com as distâncias em e as forças em com as distâncias em .