Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 161
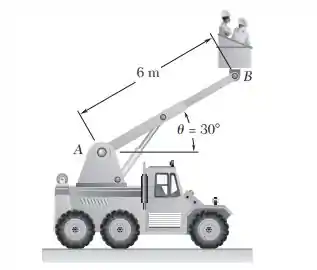
15.161. No instante mostrado na figura, o comprimento da lança AB está sendo aumentado a uma taxa constante de 0,2 m/s e a lança está sendo baixada a uma taxa constante de 0,08 rad /s. Determine (a) a velocidade do ponto B, (b) a aceleração do ponto B.
Passo 1
Hora de resolver mais um problema!
A gente pode começar o problema definindo as componentes da velocidade no ponto B.
A velocidade está a 90° da lança .
E existe uma outra velocidade que está na direção da lança com módulo de , essa informação está no enunciado.
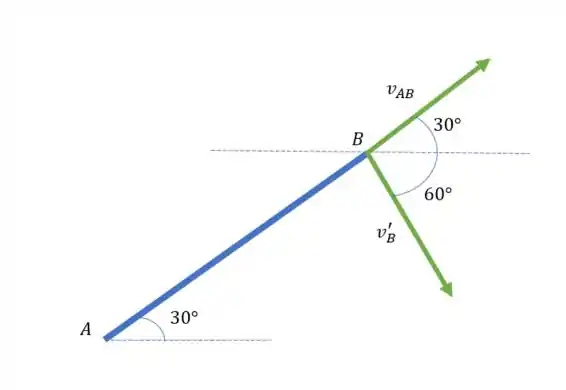
Passo 2
Então podemos fazer
Vamos separar por componentes
Isso aqui fica
E agora vamos fazer para
Isso aqui fica
Agora a gente pode calcular o módulo de
Passo 3
Para terminar de responder o item (a) só falta a gente definir o ângulo. Bom, podemos pensar nos vetores de velocidade como lados de um triângulo, onde o módulo de é a hipotenusa e e são catetos.
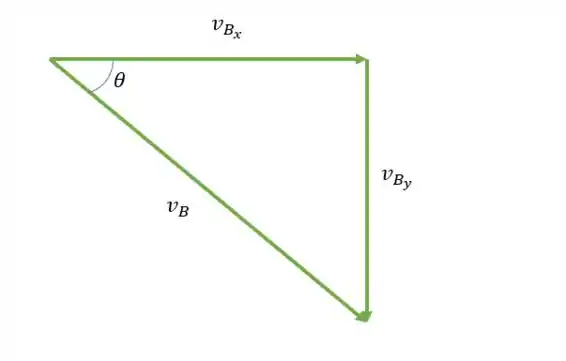
Então podemos descobrir fazendo
Então
E assim terminamos o item (a).
Passo 4
Agora vamos para o item (b).
Para calcular a aceleração podemos usar
Em que
na direção da lança., essa é a aceleração relativa entre o ponto B e a lança., essa é a aceleração de Coriolis, está perpendicular a lança.
Vamos separar as componentes
Isso fica
E para
Então o módulo é
Passo 5
Agora só falta calcular o ângulo. Vamos usar um raciocínio parecido com que usamos no item (a).
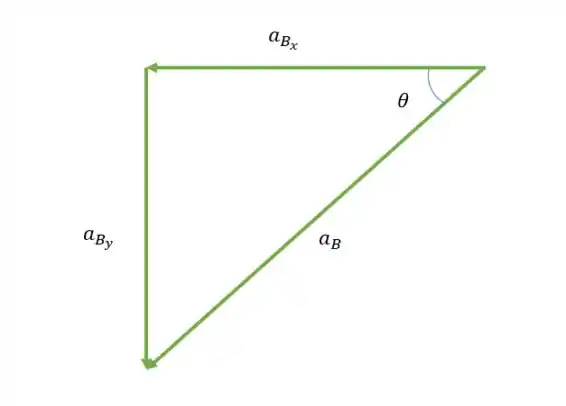
Então
E terminamos mais uma.
Resposta
