Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 17
2.15. Decomponha nas componentes que atuam ao longo dos eixos ee determine suas intensidades.
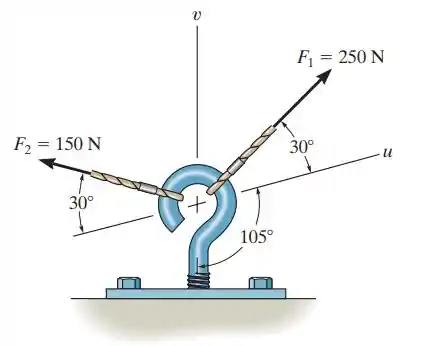
Passo 1
Vamos analisar os vetores e projetado em e projetado em , estendendo-os para formar um paralelogramo
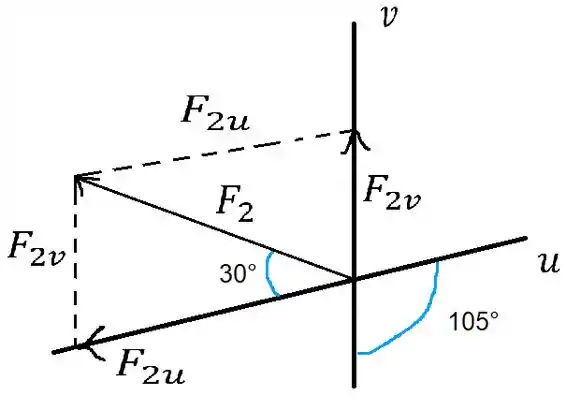
Daqui podemos extrais o seguinte triângulo
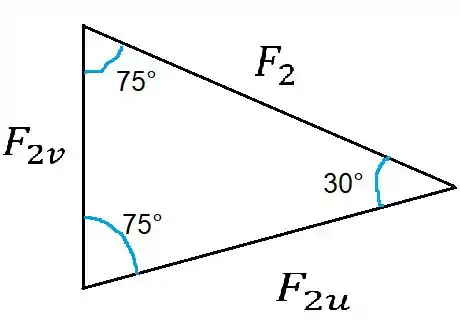
Calma que esses ângulos de 75° não surgiram do nada, eu posso explicar tudo!
Repare nessa parte do desenho
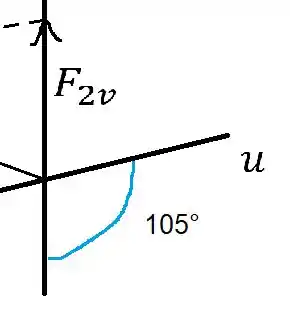
Sabemos que pra completar aquele semicírculo o ângulo entre tem que ser aquele que faça com que a soma de 180°, pois é uma reta ali.
Então o ângulo entre é 75°, logo o ângulo entre é 75°, já que são paralelos.
Agora o outro ângulo, foi tirado da propriedade que diz que a soma dos ângulos internos de um triângulo é 180°.
Passo 2
Agora só precisamos usar a lei dos senos para descobrir os componentes de
Passo 3
Só falta a componente em agora, vamos usar o mesmo método