36- O alicerce da figura é usado para apoiar uma carga de . Deternine as intensidades de e do carregamento distribuído que atua em sua base, de maneira que o equilíbrio seja mantido.

Passo 1
Precisamos encontrar a força resultante causada por essa carga e fazer com que essa força esteja em equilíbrio com a força de , em somatório de forças e em momento.
A carga pode ser dividida em duas áreas , uma retangular e outra triangular o que faz com que tenhamos o seguinte diagrama de forças abaixo.
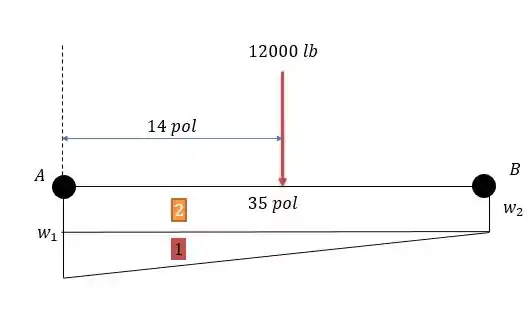
A área que é triangular gerará uma força resultante igual a sua área que vale:
Convertendo a distância para polegadas!
E que está situada em uma posição igual a:
Posição em relação ao ponto .
Já a área gerará uma força resultante igual a sua área que vale:
E que estará numa posição igual a:
Distância medida em relação ao ponto .
Passo 2
Desenhando o que fizemos no passo anterior temos:
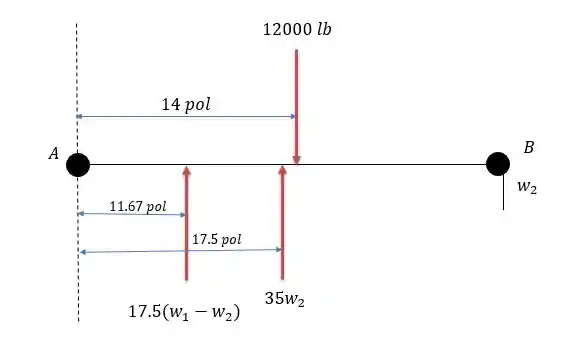
Fazendo a somatória das forças verticais temos:
Agora a somatória dos momentos em nos dará:
Esse sistema nos daria: