4.30. A prótese do quadril está sujeita à força . Determine o momento dessa força em relação ao pescoço em A e à haste em B.
Passo 1
Vamos começar esquematizando o problema
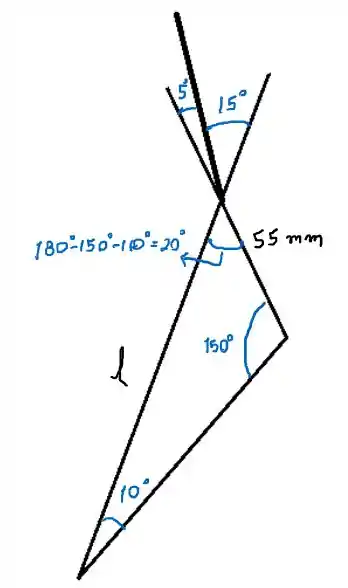
Passo 2
Vamos primeiro analisar o ponto A. Repare que o ângulo entre a linha de ação e o eixo do pescoço é
Então
O sentido é anti-horário.
Passo 3
Agora para calcular o momento B, precisamos determinar a distância entre o eixo da haste e a linha de ação da força. Para fazer isso podemos usar a lei dos senos
Então
Agora temos tudo para calcular
Ou
No sentido horário.
Resposta
O sentido é anti-horário.
O sentido é horário.